Brain Network Models

Building a brain network model (BNM) is an efficient way of simulating an in-silico version of a real brain. Two key elements compose these models: a structural connectivity matrix that serves as the skeleton of the virtual brain; and the neural mass models (NMMs) that are placed in each vertex of the skeleton to reproduce electrophysiological activity.

These BNMs allow us to perform experiments that might not be plausible with real brains either due to technical or ethical reasons. They are key to integrating evidence from multiple levels of analysis, checking for their mutual coherence, and testing the directions of causal relationships between them. They provide enough flexibility to face different problems at hand, using specific NMMs.

Surely, these models are not real brains. They are abstract representations that reproduce specific aspects of real brains, and that become useful to tackle specific research questions.

Through this tutorial, you will be provided information on how these models are built (within The Virtual Brain (TVB) simulation platform; Sanz-Leon et al., 2013) and how you can adapt them to your own research questions. We will flow from the general output of these models into the specific parts that compose them. We will show different perspectives to understand the functioning of these models.

useful info. To run code cells, you can use the "Run" button above, or use "ctrl+enter".

1. Performing a simulation

To perform a simulation, you need to import necessary packages, define simulation parameters, and run it. Let's start from the result. The output of a BNM simulation implemented in TVB is a set of timeseries. These timeseries represent the source-space signals of our in-silico brain models, with a signal per region included in the parcellation atlas used for the structural matrix. As in empirical neuroimaging studies, signals are just the raw material that will be analyzed to answer the research questions at hand.

Here, we expect to provide the tools to build such types of models. You are in charge of thinking about how these models could be applied to your specific research questions.

import os
import time
import numpy as np
from tvb.simulator.lab import *

from functions.jansen_rit_david_mine import JansenRit1995
from functions.signals import timeseriesPlot, epochingTool
from functions.fft import FFTpeaks
from functions.mixes import timeseries_spectra, timeseries_phaseplane

from plotly.subplots import make_subplots
import plotly.graph_objects as go
import plotly.offline

import warnings  # Only for the workshop; you could hide important messages.
warnings.filterwarnings("ignore")  

wd = os.getcwd()  # Define working directory
tic0 = time.time()  # Measure simulation time



timescale, simLength, transient_t = "ms", 8000, 2000  # simulation time in the NMM timescale - ms; transient time to exclude from analysis
samplingFreq = 1  # kHz - datapoints/timestep 
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints


## A1. Structural connectivity
conn = connectivity.Connectivity.from_file(wd + "/data/sub-01_AAL2_pass.zip")  # Loads structural connectivity
conn.weights = conn.scaled_weights(mode="tract")  # Scales number of streamlines using the max
conn.speed = np.array([3.9])  #(m/s) Defines conduction speed shaping delays

## A2. Neural Mass Model
m = JansenRit1995(He=np.array([3.25]), Hi=np.array([22]),
                  tau_e=np.array([10]), tau_i=np.array([20]),
                  c=np.array([1]), c_pyr2exc=np.array([135]), c_exc2pyr=np.array([108]),
                  c_pyr2inh=np.array([33.75]), c_inh2pyr=np.array([33.75]),
                  p=np.array([0.22]), sigma=np.array([0.15]),
                  e0=np.array([0.005]), r=np.array([0.56]), v0=np.array([6]))

# A3. Coupling function - How NMMs will link through structural connectivity (what variable to use and transformations to apply)
coup = coupling.SigmoidalJansenRit(a=np.array([20]), cmax=np.array([0.005]),  midpoint=np.array([6]), r=np.array([0.56]))

# A4. integrator: dt = timestep/datapoint = 1/samplingFreq(kHz=datapoints/timestep) -with timestep in NMM's timescale-.
integrator = integrators.HeunStochastic(dt=1/samplingFreq, noise=noise.Additive(nsig = np.array([0])))

# A5. Monitor - what information to extract / apply transformation (e.g. BOLD, EEG)?
mon = (monitors.Raw(), )



# B1. Configure simulation
sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

# B2. Run simulation
output = sim.run(simulation_length=simLength)
print("Simulation time: %0.2f sec  |  %0.5f sec/sim.%s" % 
      (time.time() - tic0, (time.time() - tic0)/simLength, timescale))



# C1. Extract data cutting initial transient
# output[monitor_id][time=0|data=1][timepoints, stateVars, ROIs, modes]
raw_data = output[0][1][transient_dp:, 0, :, 0].T
raw_time = output[0][0][transient_dp:]

# C2. Plot signals and spectra
timeseries_spectra(raw_data, simLength, transient_t, conn.region_labels, timescale=timescale, mode="inline")

This is the output of a whole-brain simulation. This output could lead us, for example, to perform functional connectivity analysis checking for the correlation between structural and functional connectivity matrices (Ponten et al., 2010). Or we could fit the model parameters to evaluate the impact of the local excitation-inhibition balance in brain dynamics (Deco et al., 2014), among other applications.

Being able to adapt this type of simulations to your research needs requires a deep understanding of the building blocks of the code used, as well as its flexibility to integrate and reproduce different electrophysiological phenomena.

2. The building blocks of the simulation

Several variables were defined to configure the simulation through the .Simulator() and .configure() methods of the simulator object:

sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

We will deepen each of them.

2.1 Structural connectivity

The structural connectivity is implemented in TVB as a compressed .zip file containing information regarding: the weights between regions (in weights.txt), the lengths of the tracts for those connections (tract_lengths.txt), and the names and 3d position of the regions (in centres.txt). These are the files needed for our simulation, however, additional information can be included in the zip file such as: a list of 0/1 to distinguish cortical from subcortical regions (cortical.txt), average orientations of each region with a 3D vector (average_orientations.txt), the areas of each region in millimetres (areas.txt), etc. All this information is loaded with the command "connectivity.Connectivity.from_file()" and can be accessed and used depending on the type of simulation we want to perform.

These files can be edited or replaced manually to adapt the simulation to your needs. In tvb-data, a set of samples for structural connectivity are ready to use (e.g., connectivity_76.zip) or to serve as a template to build your own.

Although these matrices are generally symmetrical due to the technical limitations of DWI and tractography algorithms. However, it is important to note that, in the case of building an asymmetric network, TVB interprets rows=to and columns=from. In other words, $w_{ij}$ refers to the weights from node j to node i.

conn = connectivity.Connectivity.from_file(wd + "/data/sub-01_AAL2_pass.zip")  # Loads structural connectivity


## Plot structural connectivity matrices: weights and tract lengths
fig = make_subplots(rows=1, cols=2, horizontal_spacing=0.22, 
                    column_titles=[r"$\text{Weights }(w_{ij})$", r"$\text{Tract lengths }(L_{ij})$"])

fig.add_trace(go.Heatmap(x=conn.region_labels, y=conn.region_labels, z=conn.weights,
                         colorscale="Turbo", colorbar=dict(x=0.4, thickness=10, title="count")), row=1, col=1)
fig.add_trace(go.Heatmap(x=conn.region_labels, y=conn.region_labels, z=conn.tract_lengths,
                         colorscale="Turbo", colorbar=dict(thickness=10, title="mm")), row=1, col=2)
fig.update_layout(height=400, width=700,
                  xaxis1=dict(tickangle=45, title="from (j)"), xaxis2=dict(tickangle=45),
                  yaxis1=dict(title="to (i)"), yaxis2=dict(showticklabels=False))
fig.show()

2.1.1 Normalize weights

Normalizing weights' matrices serves to allow for comparable simulations independent of the parameters used in tractography (e.g., number of seeds used). The scaling can be performed globally, using the maximum of the matrix as reference (mode="tract"); or locally, using the maximum weight of a region as a reference for the scaling of that region (mode="region").

conn.weights = conn.scaled_weights(mode="tract")  # Scales number of streamlines using the max

2.1.2 Conduction speed

The conduction speed ($v$) is a global parameter that interacts with the tract lengths ($L_{ij}$) to determine the delay in the propagation of a signal between regions ($d_{ij}$):

$$ d_{ij} = \frac{L_{ij}}{v} $$

In this simulation, we used 3.9 m/s as derived by Lemarechal et al. (2022).

conn.speed = np.array([3.9])  #(m/s) Defines conduction speed shaping delays

Exercise 1. Unzip sub-01_AAL2_pass.zip in Pycharm, and explore the structure of the text files inside. Then, load paupau.zip (a network with 4 nodes) from the tvb-data package, and simulate it.

""" Exercise 1. Simulate paupau.zip, and check how different configurations of weights generate different outputs.
Remember that other variables defined previously remain (e.g., model, monitor, integrator, etc.)"""


"""   Load your brand new network   """
conn = connectivity.Connectivity.from_file("paupau.zip")  # Loads structural connectivity


conn.weights = conn.scaled_weights(mode="tract")  # Scales number of streamlines using the max
conn.speed = np.array([3.9])  #(m/s) Defines conduction speed shaping delays


timescale, simLength, transient_t = "ms", 2000, 1000  # simulated timesteps in the NMM timescale - ms; transient time to exclude from analysis
samplingFreq = 1  # Hz - datapoints/timestep 
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints


tic0 = time.time()  # Measure simulation time

# B1. Configure simulation
sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

# B2. Run simulation
output = sim.run(simulation_length=simLength)
print("Simulation time: %0.2f sec  |  %0.5f sec/sim.%s" % 
      (time.time() - tic0, (time.time() - tic0)/simLength, timescale))


# C1. Extract data cutting initial transient
# output[monitor_id][time=0|data=1][timepoints, stateVars, ROIs, modes]
raw_data = output[0][1][transient_dp:, 0, :, 0].T  
raw_time = output[0][0][transient_dp:]

# C2. Plot signals and spectra
timeseries_spectra(raw_data, simLength, transient_t, conn.region_labels, timescale=timescale, mode="inline")

2.2 Neural mass model

There are different types of NMMs that reproduce different features of brain activity (see this tutorial on neural masses for an introduction) and can be implemented into a BNM. In our previous simulation, we used a Jansen-Rit NMM (Jansen & Rit, 1995) that is a biologically-plausible NMM intended to reproduce the activity of a cortical column -including pyramidal cells (y0), excitatory (y1) and inhibitory (y2) interneurons- in terms of voltage by a set of second-order differential equations:

$$ \begin{gather} \dot y_{0_i}(t) = y_{3_i}(t) \label{eq:y0}\\ \dot y_{1_i}(t) = y_{4_i}(t) \label{eq:y1}\\ \dot y_{2_i}(t) = y_{5_i}(t) \label{eq:y2}\\ \dot y_{3_i}(t) = \frac{He}{taue} \cdot S[y_{1_i}(t) - y_{2_i}(t)] - \frac{2}{ taue} \cdot y_{3_i}(t) - \frac{1}{taue^2} \cdot y_{0_i}(t) \label{eq:y3}\\ \dot y_{4_i}(t) = \frac{He}{taue} \cdot (input(t) + C_{ep} \cdot S[C_{pe} \cdot y_{0_i}(t)]) - \frac{2}{taue} \cdot y_{4_i}(t) - \frac{1}{taue^2} \cdot y_{1_i}(t) \label{eq:y4}\\ \dot y_{5_i}(t) = \frac{Hi}{taui} \cdot (C_{ip} \cdot S[C_{pi} \cdot y_{0_i}(t)]) - \frac{2}{taui} \cdot y_{5_i}(t) - \frac{1}{taui^2} \cdot y_{2_i}(t) \label{eq:y5} \end{gather} $$

Where S[v] is a sigmoidal function that converts the population averaged voltage into firing rate:

$$ \begin{gather} S\left[v\right]\ =\ \frac{e_0}{1\ +\ \exp^{r\left(v_0-v\right)}} \label{eq:sigmoid} \end{gather} $$

and the input(t) represents the sum of interregional afferences and intrinsic input ($p_i +\eta_i(t)$): $$ \begin{gather} input(t) = p_i + \eta_i(t) + g\sum_{j=1}^{n} w_{ji} \cdot S[y_{1_j}(t - d_{ji}) - y_{2_j}(t - d_{ji})] \end{gather} $$

with the following parameters:

Parameter	Value	Unit	Description
He	3.25	mV	Average excitatory synaptic gain
Hi	22	mV	Average inhibitory synaptic gain
taue	10	ms	Time Constant of excitatory PSP
taui	20	ms	Time Constant of inhibitory PSP
Cpe	135		Average synaptic contacts: pyramidals to excitatory interneurons
Cep	108		Average synaptic contacts: excitatory interneurons to pyramidals
Cpi	33.75		Average synaptic contacts: pyramidals to inhibitory interneurons
Cip	33.75		Average synaptic contacts: inhibitory interneurons to pyramidals
p	0.1085	$ms^{-1}$	Mean of random gaussian intrinsic input
$\eta$	0.022	$ms^{-1}$	Standard deviation of random gaussian intrinsic input (noise)
$e_0$	0.005	$ms^{-1}$	Maximum firing rate
r	0.56	$mV^{-1}$	Slope of the presynaptic function at $v_0$
$v_{0}$	6	mV	Potential when half the maximum firing rate is achieved
g	25		Coupling factor for inter-regional communication
s	3.9	mm/ms	Conduction speed for inter-regional communication

---

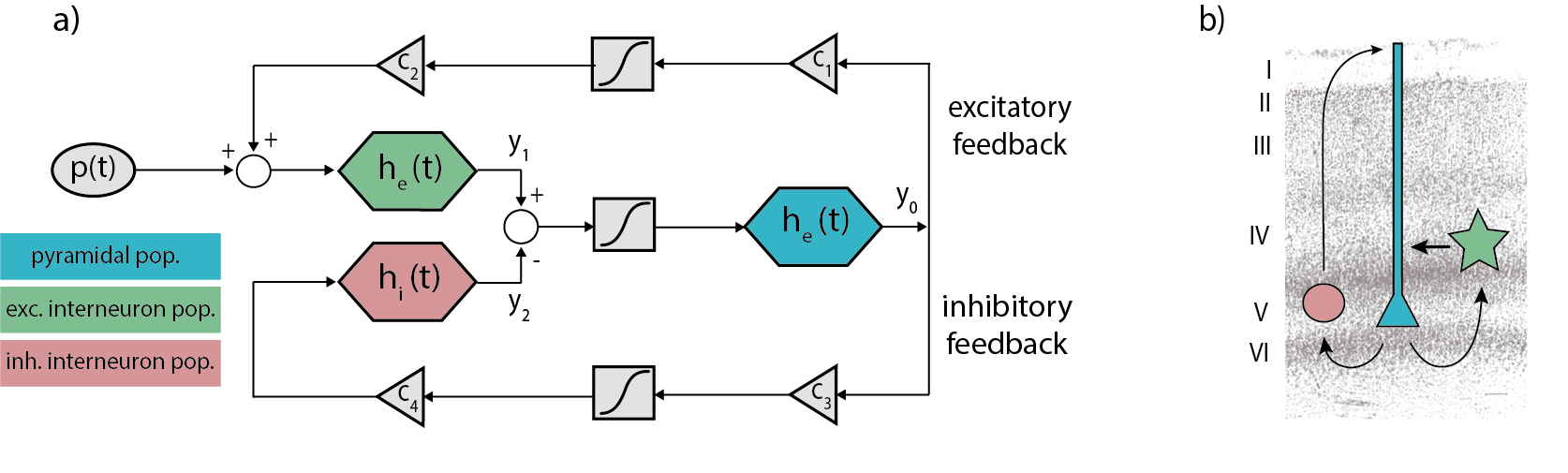
Figure 1 Schemes of the JR model. a) Block diagram depicting JR operators and modules where each color is associated with a different neural population: pyramidal (cyan), excitatory interneurons (green) and inhibitory interneuron (red). b) Histological contextualization of the cortical layers. Taken from Cabrera-Álvarez et al. (2023).

m = JansenRit1995(He=np.array([3.25]), Hi=np.array([22]),  # PSP parameters
                  tau_e=np.array([10]), tau_i=np.array([20]),
                  
                  c=np.array([1]),  # Average synaptic connections between cell types
                  c_pyr2exc=np.array([135]), c_exc2pyr=np.array([108]),
                  c_pyr2inh=np.array([33.75]), c_inh2pyr=np.array([33.75]),
                  
                  p=np.array([0.22]), sigma=np.array([0.22]),  # Intrinsic input mean (p) and std (sigma; i.e., noise)
                  
                  e0=np.array([0.005]), r=np.array([0.56]), v0=np.array([6]))  # Voltage to firing rate transfer function parameters

To deepen the behaviour of a dynamical system such as a NMM, two analytical tools from physics become insightful: the phase plane and the bifurcation diagrams. A phase plane is a graphical representation of the state variables of a dynamical system against each other. It is commonly used to analyze the qualitative behaviour of the system over time by examining the shape, stability and patterns of its trajectories. Through this type of analysis, we search for attractors (i.e., trajectories that the system tends to approach or converge to over time) such as equilibrium points in which the system remains static indefinitely, and limit cycles in which the system follows a closed trajectory repeatedly in the phase space without converging into an equilibrium point.

On the other hand, a bifurcation diagram is a graphical representation that shows the potential states of a system as a function of one parameter. For instance, NMMs are usually fed by intrinsic or extrinsic inputs such that an elevated input leads to a limit cycle (i.e., oscillatory activity), while a low input leads to an equilibrium point (no oscillation). The bifurcation point or critical point is the parameter value at which the system changes its behaviour, for example, switching from equilibrium to limit cycle state (see Deco & Jirsa, 2012).

Let's use these analytical tools to deepen the Jansen-Rit model.

2.2.1 Phase plane

The phase plane of a Jansen-Rit model is usually constructed using the state variable y0 and its derivative y3, other pairs of variables could be explored though. Here, we will use our last simulation's output to extract and plot the mentioned state variables (i.e., y0 and y3). By default, the output of simulating the JR model in TVB gathers data regarding y0, y1, y2, and y3 state variables, however, this set could be extended to the rest of state variables (i.e., y4 and y5) by changing the parameter "variables_of_interest" of the model. In our case, this is not necessary.

# C1. Extract data cutting initial transient
transient_t = 1000  # ms - simulated timesteps (in JR timescale)
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints

# Prepare the variables that feed in the phase plane
# output[monitor_id][time=0|data=1][timepoints, stateVars, ROIs, modes]
region_id = 0  # Select region of interest to plot its phase plane
y0 = output[0][1][transient_dp:, 0, region_id, 0].T  
y3 = output[0][1][transient_dp:, 3, region_id, 0].T  
t = output[0][0][transient_dp:] 

timeseries_phaseplane(t, y0, y3, mode="inline", params=["Voltage (mV) <br> y0", "y3"], speed=4)

Exercise 2. Explore what happens when we include in the analysis the initial transient (<1000 ms)

""" Exercise 2. Explore what happens when we include the initial transient. """

2.2.2 Bifurcation diagram

As stated before, in a dynamical system a bifurcation occurs when a change in a parameter produces a change in the system's behaviour. NMMs tend to present supercritical Hopf bifurcations for the input parameter. A Hopf bifurcation is specifically the bifurcation in which an equilibrium state changes into an oscillation, and is supercritical because the oscillatory behaviour happens above the critical point.

The 2D representation of a NMM bifurcation is usually made by representing the maximum and minimum voltage of a simulation for each value of the bifurcation parameter being explored (see Grimbert & Faugeras, 2006). Here, we will add a 3D representation of the bifurcation diagram including phase planes as exposed previously.

## Bifurcation diagrams: Exploring the input parameter (p)
bifparam_vals = np.linspace(0, 0.2, 15)

simLength, transient_t, region_id = 5000, 4500, 0
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints


out2D, out3D = [], []
for i, bifparam in enumerate(bifparam_vals):

    tic0 = time.time()

    ## A2. Neural Mass Model
    m.p = np.array([bifparam])
    
    # A3. Coupling function
    coup.a = np.array([0])

    # B1. Configure simulation
    sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup, integrator=integrator, monitors=mon)
    sim.configure()

    # B2. Run simulation
    output = sim.run(simulation_length=simLength)
    print("Simulation %i/%i  .  time: %0.2f sec  |  %0.5f sec/sim.%s" %
          (i+1, len(bifparam_vals), time.time() - tic0, (time.time() - tic0)/simLength, timescale), end="\r")


    # output[monitor_id][time=0|data=1][timepoints, stateVars, ROIs, modes]
    out2D.append([bifparam, min(output[0][1][transient_dp:, 0, region_id, 0].T), max(output[0][1][transient_dp:, 0, region_id, 0].T)])
    out3D.append([bifparam, output[0][1][transient_dp:, 0, region_id, 0].T, output[0][1][transient_dp:, 3, region_id, 0].T])

print("- Done ! -")
out2D, out3D = np.asarray([out2D])[0], np.asarray([out3D])[0]

## FIGURES :: Bifurcation in 2D/3D
fig = make_subplots(rows=2, cols=1, specs=[[{"type": "scene"}], [{}]], row_heights=[0.85, 0.15], vertical_spacing=0.05)

# 2D representation
fig.add_trace(go.Scatter(x=out2D[:, 0], y=out2D[:, 1], showlegend=False, marker=dict(color="black")), row=2, col=1)
fig.add_trace(go.Scatter(x=out2D[:, 0], y=out2D[:, 2], showlegend=False, marker=dict(color="black")), row=2, col=1)

# 3D representation
for i, p in enumerate(bifparam_vals):
    fig.add_trace(go.Scatter3d(x=[out3D[i, 0]]*len(out3D[i, 1]), y=out3D[i, 2], z=out3D[i, 1],
                               showlegend=False, marker=dict(size=2)), row=1, col=1)

fig.update_layout(template="plotly_white", height=700, width=700,
                  xaxis=dict(title="p (input)"), yaxis=dict(title="Voltage (mV) <br> min-max <br> y0"),
                  scene1=dict(xaxis=dict(title="p (input)", autorange="reversed"), yaxis=dict(title="y3"), zaxis=dict(title="Voltage (mV) <br> y0"),
                              camera=dict(eye=dict(x=0.7, y=2, z=0.5), center=dict(z=-0.25))))
plotly.offline.iplot(fig)

Exercise 3. Remove noise from simulations and re-draw the phase plane for a JR NMM.

""" Exercise 3. Remove noise from simulations and re-draw the phase plane for a JR NMM. """

2.3 Coupling function

The coupling function mediates how structurally connected neural masses influence each other (e.g., what state variables should be used? Should they be transformed? How strong are the mutual influences defined in the SC matrix?). The parameters of this function are applied globally to all the simulated connections. Different NMMs may use different coupling functions: from a simple linear scaling of a state variable to a sigmoidal transformation of a combination of state variables.

In the case of the JR model, the afference to a neural mass is considered to be the delayed activity of the neighbouring pyramidal cells in terms of firing rate, scaled interregionally by SC weights ($w_{ij}$) and globally by a coupling factor (a). It represents the third element of the input(t) as defined above:

$$ \begin{gather} \color{lightgray}{input(t) = p_i + \eta_i(t) + \color{black}{ a\sum_{j=1}^{n} w_{ij} \cdot S[y_{1_j}(t - d_{ij}) - y_{2_j}(t - d_{ij})]}} \end{gather} $$

Where $S[v]$, again represents the firing rate of pyramidal cells using the same sigmoidal function applied inside the NMM for communicating cellular subpopulations:

$$ \begin{gather} S\left[v\right]\ =\ \frac{v_{\max}}{1\ +\ \exp^{r\left(v_0-v\right)}} \label{eq:sigmoid} \end{gather} $$

Note that the coupling parameters defined inside the model for subpopulation communication (see the values for parameters e0, v0 and r) coincide with the parameters defined for interregional coupling (see the values for parameters cmax, midpoint and r).

# A3. Coupling function - How NMMs will link through structural connectivity (what variable to use and transformations to apply)
coup = coupling.SigmoidalJansenRit(a=np.array([20]), cmax=np.array([0.005]),  midpoint=np.array([6]), r=np.array([0.56]))

Exercise 4. Is the coupling factor a bifurcation parameter? Design an experiment to answer this question. Then, adapt the code provided above to simulate and represent graphically your response. Use p=0.09 and coupling range=[0-30].

"""
Exercise 4. Is the coupling factor a bifurcation parameter? Re-use the code provided above
"""

## FIGURES :: Bifurcation in 2D/3D
fig = make_subplots(rows=2, cols=1, specs=[[{"type": "scene"}], [{}]], row_heights=[0.85, 0.15], vertical_spacing=0.05)

# 2D representation
fig.add_trace(go.Scatter(x=out2D[:, 0], y=out2D[:, 1], showlegend=False, marker=dict(color="black")), row=2, col=1)
fig.add_trace(go.Scatter(x=out2D[:, 0], y=out2D[:, 2], showlegend=False, marker=dict(color="black")), row=2, col=1)

# 3D representation
for i, p in enumerate(bifparam_vals):
    fig.add_trace(go.Scatter3d(x=[out3D[i, 0]]*len(out3D[i, 1]), y=out3D[i, 2], z=out3D[i, 1],
                               showlegend=False, marker=dict(size=2)), row=1, col=1)

fig.update_layout(template="plotly_white", height=700, width=700,
                  xaxis=dict(title="Coupling factor"), yaxis=dict(title="Voltage (mV) <br> min-max <br> y0"),
                  scene1=dict(xaxis=dict(title="Coupling factor", autorange="reversed"), yaxis=dict(title="y3"), zaxis=dict(title="Voltage (mV) <br> y0"),
                              camera=dict(eye=dict(x=0.7, y=2, z=0.5), center=dict(z=-0.25))))
plotly.offline.iplot(fig)

2.4 Integrator

The integrator defines the method used for solving the systems of differential equations. There are several integration methods available in TVB. We will comment on two of them: Euler's and Heun's methods. Euler's method calculates the trajectory of a dynamical system based just on its derivatives in time. On the other hand, Heun's method is known as an improved version of Euler's, it takes several consecutive derivatives to estimate the next trajectory step and minimize integration errors. This makes Heun's method more stable and precise, at the cost of being more computationally expensive. Both methods could be implemented in a deterministic or stochastic fashion, allowing for the introduction of noise and random initial states in the simulation.

An important parameter of the integrator is the step size of the derivatives (i.e., dt). The larger the step size, the less simulated datapoints and the faster the computation times. However, is important to choose an adequate step size for the NMM used to avoid simulation instabilities. Note that different models may be defined at different timescales: a timestep for model A may represent a millisecond while a timestep for another model may represent a second. Additionally, in the case of stochastic integration, the magnitude of the implemented noise could also lead to instabilities. So, whenever having issues implementing a new neural mass model, check whether the integration method, the step size, or the noise magnitude may be generating instabilities.

With an stochastic integrator, noise is added at each integration timestep for each state variable of the system. In the case of the original JR, the noise is implemented just thorugh the intrinsic input (i.e., p + $\eta$) to the excitatory interneurons (y1). This is a much more controlled implementation of noise than the stochastic integration. Therefore, for JR, we are not using the integrator noise. However, we use the stochastic Heun's integrator for another relevant reaseon, the randomization of initial state variables (note that each simulation produces a different temporal trace).

Exercise 5. Explore the effects of different noise implementation: NMM vs integrator.

"""Exercise 5. Explore the effects of different noise implementation: NMM vs integrator."""

## A2. Neural Mass Model
m = JansenRit1995(He=np.array([3.25]), Hi=np.array([22]),  # PSP parameters
                  tau_e=np.array([10]), tau_i=np.array([20]),
                  
                  c=np.array([1]),  # Average synaptic connections between cell types
                  c_pyr2exc=np.array([135]), c_exc2pyr=np.array([108]),
                  c_pyr2inh=np.array([33.75]), c_inh2pyr=np.array([33.75]),
                  
                  p=np.array([0.22]), sigma=np.array([0.22]),  # Intrinsic input mean (p) and std (sigma; i.e., noise)
                  
                  e0=np.array([0.005]), r=np.array([0.56]), v0=np.array([6]))  # Voltage to firing rate transfer function parameters


# A4. integrator: dt = timestep/datapoint = 1/samplingFreq(Hz=datapoints/timestep) -with timestep in NMM's timescale-.
integrator = integrators.HeunStochastic(dt=1/samplingFreq, noise=noise.Additive(nsig=np.array([0])))


tic0 = time.time()

simLength, transient_t, region_id = 3000, 1000, 0
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints    
    
# B1. Configure simulation
sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

# B2. Run simulation
output = sim.run(simulation_length=simLength)
print("Simulation time: %0.2f sec  |  %0.5f sec/sim.%s" % (time.time() - tic0, (time.time() - tic0)/simLength, timescale))


# C1. Extract data cutting initial transient
# output[monitor_id][time=0|data=1][timepoints, stateVars, ROIs, modes]
raw_data = output[0][1][transient_dp:, 0, :, 0].T  
raw_time = output[0][0][transient_dp:]

# C2. Plot signals and spectra
timeseries_spectra(raw_data, simLength, transient_t, conn.region_labels, timescale=timescale, mode="inline")

2.5 Monitors

Monitors define what output will be saved from the simulations, and whether they must be transformed somehow. A BNM simulation generates a signal for each state variable of each region implemented in the model. These signals are supposed to be source signals located inside the virtual brain. From the simulations performed earlier, we have extracted directly the raw output of the JR state variables. However, sometimes becomes convenient to perform some transformation to this output. For instance, you could prefer to downsample the temporal traces due to memory load (use monitors.TemporalAverage()), or you could prefer to see the signals in the channel space of a M/EEG system (use monitors.EEG()). The monitors perform these transformations online during the simulations.

Some of these monitors become more useful in the context of surface-based simulations where larger amounts of data may require spatial or temporal averaging, or it may become more interesting to transform source data to fMRI, MEG, or EEG recording type.

# A5. Monitor - what information to extract / apply transformation (e.g. BOLD, EEG)?
mon = (monitors.Raw(), monitors.TemporalAverage(period=20),)

2.6 Additional blocks

There are two additional blocks that were not included in our simulator object but are useful for specific applications: the surface and the stimulus. The surface refers to a mesh of the cortex that is used to extend the spatial domain of the BNM to a surface model. The stimulus allows to implement a simulated stimulation to the virtual brain. This stimulus would be directly summed up during integration scheme to the specified state variable. Different types of stimulation could be modeled and implemented (e.g., tDCS, tACS, TMS, DBS).

3. BNM Stimulation

                To be continued... (SEPNECA 2024?)

4. Surfaced-BNMs

                To be continued... (SEPNECA 2024?)

· More exercises

Usually, coding for any application (in our case computational neuroscience) is developed in an integrated development environment (IDE), a software that provides useful tools to write and debug code, such as Spyder or Pycharm. Now, go to Pycharm to work on the last assignments.

Exercise 6. Build, simulate and plot the JR-BNM in Pycharm. Use the code and tools provided.

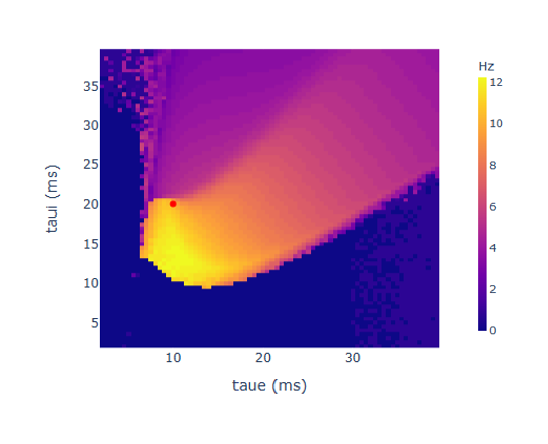
Exercise 7 (optional). A) Explore the behaviour of a single JR-NMM when varying its parameters taue and taui. As time constants, they have a strong impact on the oscillatory frequency (see chart below). How would you explore their impact? Hint: get some inspiration from functions/mixes.py. B) Explore the behaviour of parameters He and Hi (amplitude of PSP). Do they affect the frequency of oscillation?

Exercise 8. Using the project bar in Pycharm, look in the external libraries for the tvb packages. Could you find the code for the Linear coupling function? How many model types are implemented in TVB? What's the size (kB) of the paupau connectivity in tvb-data?

Exercise 9. Build, simulate and plot a BNM with a neural mass of your interest, and different from JR-NMM.

Exercise 10. Give a thought on whether these types of models could help you in your research. What could you do with a virtual version of your participants' brains? What hypothesis would you test on a generic virtual brain? What limitations do you expect from using these models?

· Useful resources

installation - To use TVB, you need a Python version installed. Python includes a package distribution system called pipy. You could use it to install the necessary packages by typing in terminal: pip install whatever-package-name; for instance, pip install tvb-library, pip install tvb-data, or pip install plotly.

• TVB Documentation
• DSI studio tutorials for a user friendly and accurate tool to extract SC matrices in limited time (see Maier-Hein, 2017 for a pipeline comparison).
• EBRAINS platform for datasets, brain atlases, modeling tools, etc.

· References

Breakspear, M. (2017). Dynamic models of large-scale brain activity. In Nature Neuroscience (Vol. 20, Issue 3, pp. 340–352). Springer Science and Business Media LLC. https://doi.org/10.1038/nn.4497

Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015). Mathematical framework for large-scale brain network modeling in The Virtual Brain. In NeuroImage (Vol. 111, pp. 385–430). Elsevier BV. https://doi.org/10.1016/j.neuroimage.2015.01.002

On the construction of BNMs:

Schirner, M., Rothmeier, S., Jirsa, V. K., McIntosh, A. R., & Ritter, P. (2015). An automated pipeline for constructing personalized virtual brains from multimodal neuroimaging data. In NeuroImage (Vol. 117, pp. 343–357). Elsevier BV. https://doi.org/10.1016/j.neuroimage.2015.03.055

Studies using BNMs:

Cabral, J., Castaldo, F., Vohryzek, J., Litvak, V., Bick, C., Lambiotte, R., Friston, K., Kringelbach, M. L., & Deco, G. (2022). Metastable oscillatory modes emerge from synchronization in the brain spacetime connectome. In Communications Physics (Vol. 5, Issue 1). Springer Science and Business Media LLC. https://doi.org/10.1038/s42005-022-00950-y

Jirsa, V., Wang, H., Triebkorn, P., Hashemi, M., Jha, J., Gonzalez-Martinez, J., Guye, M., Makhalova, J., & Bartolomei, F. (2023). Personalised virtual brain models in epilepsy. In The Lancet Neurology (Vol. 22, Issue 5, pp. 443–454). Elsevier BV. https://doi.org/10.1016/s1474-4422(23)00008-x

Petkoski, S., Ritter, P., & Jirsa, V. K. (2023). White-matter degradation and dynamical compensation support age-related functional alterations in human brain. In Cerebral Cortex (Vol. 33, Issue 10, pp. 6241–6256). Oxford University Press (OUP). https://doi.org/10.1093/cercor/bhac500

Some on the stimulation of BNMs:

Merlet, I., Birot, G., Salvador, R., Molaee-Ardekani, B., Mekonnen, A., Soria-Frish, A., Ruffini, G., Miranda, P. C., & Wendling, F. (2013). From Oscillatory Transcranial Current Stimulation to Scalp EEG Changes: A Biophysical and Physiological Modeling Study. In G. R. Barnes (Ed.), PLoS ONE (Vol. 8, Issue 2, p. e57330). Public Library of Science (PLoS). https://doi.org/10.1371/journal.pone.0057330

Muldoon, S. F., Pasqualetti, F., Gu, S., Cieslak, M., Grafton, S. T., Vettel, J. M., & Bassett, D. S. (2016). Stimulation-Based Control of Dynamic Brain Networks. In C. C. Hilgetag (Ed.), PLOS Computational Biology (Vol. 12, Issue 9, p. e1005076). Public Library of Science (PLoS). https://doi.org/10.1371/journal.pcbi.1005076

Some more using Surface-based BNM:

Spiegler, A., Abadchi, J. K., Mohajerani, M., & Jirsa, V. K. (2020). In silico exploration of mouse brain dynamics by focal stimulation reflects the organization of functional networks and sensory processing. In Network Neuroscience (Vol. 4, Issue 3, pp. 807–851). MIT Press. https://doi.org/10.1162/netn_a_00152

Spiegler, A., Hansen, E. C. A., Bernard, C., McIntosh, A. R., & Jirsa, V. K. (2016). Selective Activation of Resting-State Networks following Focal Stimulation in a Connectome-Based Network Model of the Human Brain. In eneuro (Vol. 3, Issue 5, p. ENEURO.0068-16.2016). Society for Neuroscience. https://doi.org/10.1523/eneuro.0068-16.2016