0. Prepare simulation framework

First, set up the BNM simulation framework (TVB) to focus just on NMMs later. If you come from the tutorial on Brain Network Models, I recommend you load the small 3 nodes' structural network that you may have constructed, changing the path for structural connectivity in the code below. Also, I would recommend you read the whole BNM tutorial before starting this one. Remember that the optimal integration time step (dt) and the internode coupling function may vary with the NMM used.

Now, execute the code below to get ready to focus on Neural Masses.

import os
import time
import numpy as np
from tvb.simulator.lab import *

from functions.jansen_rit_david_mine import JansenRit1995
from functions.signals import timeseriesPlot, epochingTool
from functions.fft import FFTpeaks
from functions.mixes import timeseries_spectra, timeseries_phaseplane, kuramoto_polar

from jupyter_dash import JupyterDash
from dash import Dash, html, dcc, callback, Output, Input
from plotly.subplots import make_subplots
import plotly.graph_objects as go
import plotly.offline

import warnings
warnings.filterwarnings("ignore")

wd = os.getcwd()  # Define working directory

## A1. Structural connectivity
conn = connectivity.Connectivity.from_file("paupau.zip")  # Loads structural connectivity
conn.weights = conn.scaled_weights(mode="tract")  # Scales number of streamlines using the max
conn.speed = np.array([3.9])  #(m/s) Defines conduction speed shaping delays

# A5. Monitor - what information to extract / apply transformation (e.g. BOLD, EEG)?
mon = (monitors.Raw(),)

Neural Mass Models

A neural mass model is a set of equations that describe the dynamics and behaviour of a large population of interconnected neurons as a collective entity. Instead of focusing on the detailed activity of individual neurons, a neural mass model provides a simplified representation of the average behaviour of the population. These models often include subpopulations to reproduce functional and biological features of the neural tissue, for instance, excitatory and inhibitory subpopulations and describing their interactions. A neural mass aims to capture the macroscopic behaviour of the population, such as the overall firing rate or synchronization patterns, rather than the precise spiking activity of individual neurons. They are especially useful for studying phenomena at a larger scale, such as cortical columns or brain regions. The rationale behind this approach has been previously discussed:

“ ... most of what is known about the operation of the brain in relation to behavior has come from studies based on stimulation, field potential recordings or ablation of masses of brain tissue containing tens or hundreds millions of neurons. ... the numbers are too great to conceive the modeling in terms of finite numbers of cells.” Freeman (1972)

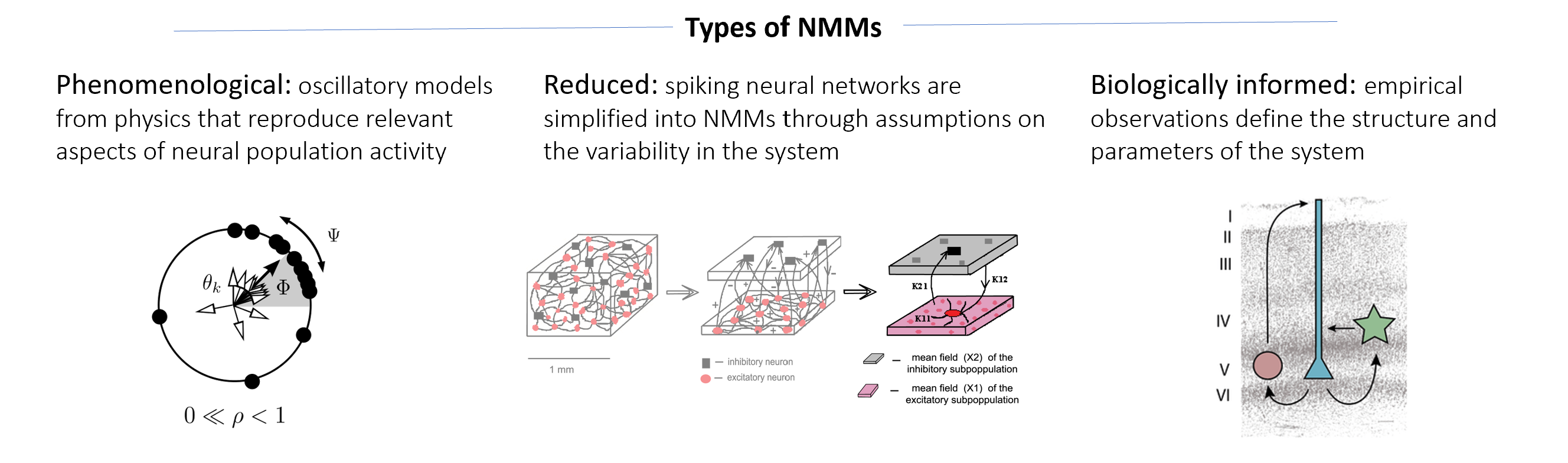
1. Phenomenological models

These types of models are the most abstract and mathematically simple NMMs. They come from physics as basic formulations to describe and explain (coupled) oscillatory systems. Although they are not inspired by biological features, they capture phenomenologically the oscillatory behaviour of a neural population. Their simplicity makes them computationally light in terms of simulation time and memory consumption. More importantly, their mathematical formulations tend to focus on specific phenomenological aspects of oscillatory systems raising the opportunity to explore their behaviour and interactions on neural networks.

Let's dig into a couple of them.

1.1 Stuart-Landau (1960)

The Stuart-Landau model was developed as a mathematical framework to study instabilities and bifurcations (i.e., the transitions from order to chaos) in physical systems in the context of fluid dynamics. It was named after two scientists, J. T. Stuart and L. D. Landau, who independently worked on this model around the same time. Their elegant formulation was written to operate in the complex space: $\color{darkslategray}{\dot Z_n = Z_n \cdot [a + iw - Z^{2}_{n}]}$. Following the literature from physics, Deco et al., (2017) reformulated the equation into cartesian coordinates (as implemented in TVB):

$$ \begin{gather} \dot{x}_{i} &= (a_{i} - x_{i}^{2} - y_{i}^{2})x_{i} - {\omega}{i}y_{i}\\ \dot{y}_{i} &= (a_{i} - x_{i}^{2} - y_{i}^{2})y_{i} + {\omega}{i}x_{i} \end{gather} $$

Note that both formulations of the model have the same two parameters:

Parameter	Description
$a$	Bifurcation parameter
$w$	Oscillatory frequency

The model shows a bifurcation over parameter "a" (see below) in which a transition from a fixed point state (a<0) to a limit cycle state (a>0) happens at a=0. This type of bifurcation is called Supercritical Hopfield. In TVB, this model is implemented using its cartesian formulation and named after its bifurcation (i.e., SupHopf model).

## A2. Neural Mass Model
m = models.SupHopf(a=np.array([-0.5]), omega=np.array([2*np.pi*10])) # omega as angular frequency
m.variables_of_interest=("x", "y")  # By default only x is recorded, but we need y for phase plane

# A3. Coupling function - How NMMs will link through structural connectivity 
coup = coupling.Linear(a=np.array([0]))



""" Integration time settings """
timescale, simLength, transient_t = "sec", 3, 1  # timesteps in NMM's timescale; transient time to exclude
samplingFreq = 1000  # Hz - datapoints / timestep 
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints

# A4. integrator: dt = timestep/datapoint = 1/samplingFreq(Hz=datapoints/timestep)
integrator = integrators.HeunStochastic(dt=1/samplingFreq, noise=noise.Additive(nsig = np.array([0])))



# B1. Configure simulation
tic0 = time.time()
sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

# B2. Run simulation
output = sim.run(simulation_length=simLength)
print("Simulation time: %0.2f sec  |  %0.2f sec/sim.%s" % 
      (time.time() - tic0, (time.time() - tic0)/simLength, timescale))


# C1. Extract data
raw_data = output[0][1][transient_dp:, 0, :, 0].T
raw_time = output[0][0][transient_dp:]

# C2. Plot signals and spectra
timeseries_spectra(raw_data, simLength, transient_t, conn.region_labels, yaxis="x",
                   timescale=timescale, mode="inline", title="Stuart-Landau (1960)")

##  Phase plane
# C1. Extract data cutting initial transient
transient_t = 1  # s - simulated timesteps
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints

# Prepare the variables that feed in the phase plane
# output[monitor_id][time=0|data=1][timepoints, stateVars, ROIs, modes]
region_id = 0  # Select region of interest to plot its phase plane
x = output[0][1][transient_dp:, 0, region_id, 0].T  
y = output[0][1][transient_dp:, 1, region_id, 0].T  
t = output[0][0][transient_dp:] 

timeseries_phaseplane(t, x, y, mode="inline", params=["x", "y"], speed=4)

## Simulate the bifurcation: Exploring the input parameter (p)
bifparam_vals, simLength, transient_t, region_id = np.linspace(-15, 15, 30), 5, 4.5, 0
transient_dp = int(transient_t * samplingFreq)  # convert transient time into number of datapoints


out2D, out3D = [], []
for i, bifparam in enumerate(bifparam_vals):

    tic0 = time.time()

    ## A2. Neural Mass Model
    m.a = np.array([bifparam])
    
    # A3. Coupling function
    coup.a = np.array([0])

    # B1. Configure simulation
    sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup, integrator=integrator, monitors=mon)
    sim.configure()

    # B2. Run simulation
    output = sim.run(simulation_length=simLength)
    print("Simulation %i/%i  .  time: %0.2f sec  |  %0.2f sec/sim.%s" %
          (i+1, len(bifparam_vals), time.time() - tic0, (time.time() - tic0)/simLength, timescale), end="\r")


    # output[monitor_id][time=0|data=1][timepoints, stateVars, ROIs, modes]
    out2D.append([bifparam, min(output[0][1][transient_dp:, 0, region_id, 0].T), max(output[0][1][transient_dp:, 0, region_id, 0].T)])
    out3D.append([bifparam, output[0][1][transient_dp:, 0, region_id, 0].T, output[0][1][transient_dp:, 1, region_id, 0].T])

print("- Done ! -")
out2D, out3D = np.asarray([out2D])[0], np.asarray([out3D])[0]

## Plot bifurcation in 2D/3D
fig = make_subplots(rows=2, cols=1, specs=[[{"type": "scene"}], [{}]], row_heights=[0.8, 0.2], vertical_spacing=0.05)

# 2D representation
fig.add_trace(go.Scatter(x=out2D[:, 0], y=out2D[:, 1], showlegend=False, marker=dict(color="black")), row=2, col=1)
fig.add_trace(go.Scatter(x=out2D[:, 0], y=out2D[:, 2], showlegend=False, marker=dict(color="black")), row=2, col=1)

# 3D representation
for i, bifparam in enumerate(bifparam_vals):
    fig.add_trace(go.Scatter3d(x=[out3D[i, 0]]*len(out3D[i, 1]), y=out3D[i, 2], z=out3D[i, 1],
                               showlegend=False, marker=dict(size=2)), row=1, col=1)

fig.update_layout(template="plotly_white", height=600, width=600,
                  xaxis=dict(title="a (Bifurcation parameter)"), yaxis=dict(title="x"),
                  scene1=dict(xaxis=dict(title="a (Bifurcation parameter)", autorange="reversed"), 
                              yaxis=dict(title="y"), zaxis=dict(title="x"),
                              camera=dict(eye=dict(x=1.2, y=2.45, z=0.5), center=dict(x=0.3, z=-0.25))))
plotly.offline.iplot(fig)

References

Stuart, J. T. (1960). On the non-linear mechanics of wave disturbances in stable and unstable parallel flows Part 1. The basic behaviour in plane Poiseuille flow. In Journal of Fluid Mechanics (Vol. 9, Issue 3, pp. 353–370). Cambridge University Press (CUP). https://doi.org/10.1017/s002211206000116x

---

Deco, G., Kringelbach, M. L., Jirsa, V. K., & Ritter, P. (2017). The dynamics of resting fluctuations in the brain: metastability and its dynamical cortical core. In Scientific Reports (Vol. 7, Issue 1). Springer Science and Business Media LLC. https://doi.org/10.1038/s41598-017-03073-5

Cabral, J., Castaldo, F., Vohryzek, J., Litvak, V., Bick, C., Lambiotte, R., Friston, K., Kringelbach, M. L., & Deco, G. (2022). Metastable oscillatory modes emerge from synchronization in the brain spacetime connectome. In Communications Physics (Vol. 5, Issue 1). Springer Science and Business Media LLC. https://doi.org/10.1038/s42005-022-00950-y

Selivanov, A. A., Lehnert, J., Dahms, T., Hövel, P., Fradkov, A. L., & Schöll, E. (2012). Adaptive synchronization in delay-coupled networks of Stuart-Landau oscillators. In Physical Review E (Vol. 85, Issue 1). American Physical Society (APS). https://doi.org/10.1103/physreve.85.016201

1.2 Kuramoto (1975)

The Kuramoto model, proposed by Yoshiki Kuramoto in 1975, is a mathematical model that aims to capture the synchronization behaviour observed in a system of coupled oscillators. It describes the dynamics of a set of oscillators characterized by its own intrinsic frequency and phase. As they are connected, the model assumes that each oscillator influences each other, causing their phases to align or synchronize over time. The Kuramoto model has gained significant attention due to its simplicity and its ability to capture fundamental aspects of synchronization observed in real-world systems.

$$ \dot \theta_i = w_i + \frac{K}{N} \sum^{N}_{j=1} sin(\theta_j - \theta_i) $$

Parameter	Description
$w$	Oscillatory frequency
$K$	Coupling strength
$N$	Number of coupled nodes

## A2. Neural Mass Model
m = models.Kuramoto(omega=np.array([2*np.pi*10])) # omega as angular frequency

# A3. Coupling function - How NMMs will link through structural connectivity 
coup = coupling.Kuramoto(a=np.array([0.9]))


""" Integration time settings """
timescale, simLength, transient_t = "sec", 6, 2  # timesteps in NMM's timescale; transient time to exclude
samplingFreq = 1000  # Hz - datapoints / timestep 
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints

# A4. integrator: dt = timestep/datapoint = 1/samplingFreq(Hz=datapoints/timestep)
integrator = integrators.HeunStochastic(dt=1/samplingFreq, noise=noise.Additive(nsig = np.array([0.5])))



## A1. Structural connectivity
conn = connectivity.Connectivity.from_file("paupau.zip")  # Loads structural connectivity
conn.weights = conn.scaled_weights(mode="tract")  # Scales number of streamlines using the max
conn.speed = np.array([3.9])  #(m/s) Defines conduction speed shaping delays



# B1. Configure simulation
tic0 = time.time()
sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

# B2. Run simulation
output = sim.run(simulation_length=simLength)
print("Simulation time: %0.2f sec  |  %0.2f sec/sim.%s" % 
      (time.time() - tic0, (time.time() - tic0)/simLength, timescale))


# C1. Extract data
raw_data = output[0][1][transient_dp:, 0, :, 0].T
raw_time = output[0][0][transient_dp:]

# C2. Plot signals and spectra
timeseries_spectra(raw_data, simLength, transient_t, conn.region_labels, yaxis="Phase (rad)",
                   timescale=timescale, mode="inline", title="Kuramoto (1975)")

This is a typical output of a Kuramoto simulation. Oscillations are not visible at first sight, however, they are embedded into the phase expressed in radians. One cycle is represented by a phase of $2\pi$ ~ 6.28. In the following, we will wrap the phase to a range between 0 and 2$\pi$, meaning that when the phase angle exceeds this range it is "wrapped" or adjusted to stay within the desired interval, allowing for proper calculations or comparisons involving phase angles.

# C3. Lets wrap the phase
fig = go.Figure()

for i, signal_phase in enumerate(raw_data):
    warped_phase = (signal_phase % (2*np.pi))
    fig.add_trace(go.Scatter(x=raw_time, y=warped_phase, name=conn.region_labels[i]))
    
fig.update_layout(template="plotly_white", height=300, width=600,
                  yaxis=dict(title="Phase (rad)"), xaxis=dict(title="Time (seconds)"))
fig.show()

This way, we begin to understand the presence of an oscillatory phenomenon. However, we will take a further step in that direction by placing these phases into a polar plot and calculating the degree of synchrony between oscillators using the Kuramoto order parameter:

$$ R = \frac{1}{N} \sum^{N}_{j=1} e^{i\theta_j} $$

The magnitude of the Kuramoto order parameter, |R|, indicates the overall coherence or synchronization of the oscillators. If |R| is close to 0, it suggests a lack of synchronization, whereas if |R| is close to 1, it indicates strong synchronization. The angle of the Kuramoto order parameter provides information about the average phase of the oscillators.

By calculating the Kuramoto order parameter (KO) over time or in different conditions, one can track the evolution of synchronization and analyze the effects of various parameters on the synchronization behaviour of the oscillators in the system.

# C4. Polar plot for phases and Kuramoto Order parameter
speed = 15  # Speed up animation [1Hz~x50-10s; 10Hz~x15?-1s]
kuramoto_polar(raw_data, raw_time, speed, timescale, mode="inline")

Kuramoto is a simple but very interesting model, let's explore it a little bit further.

Exercise 1. Explore the following situations: 1.1) Remove noise; 1.2) Implement homogeneous tract lengths; 1.3) Disconnect the oscillators. What parameters resulted in a larger rise and more stable KO?

Exercise supp (optional). Kuramoto order parameter measures overall synchronization in the network but is not capable of capturing delayed synchronization. Phase Locking Value (PLV) can do it. Following the equation below, implement a function to calculate PLV and measure the delayed synchrony between regions varying parameter K and noise. $$ PLV_{ij} = \frac{1}{N} \Bigg|\sum_{n=1}^{N} e^{i(\phi_i(t)-\phi_j(t))}\Bigg| $$ Where N stands for the number of data points.

""" Exercise 1. Exploring Kuramoto model """

# conn.tract_lengths = 50 * np.ones((4,4))  # Homogeneous tract lengths (50 mm) for a network of 4 nodes

References

Kuramoto, Y. (1975). Self-entrainment of a population of coupled non-linear oscillators. In International Symposium on Mathematical Problems in Theoretical Physics (pp. 420–422). Springer-Verlag. https://doi.org/10.1007/bfb0013365

---

Strogatz, S. H. (2000). From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. In Physica D: Nonlinear Phenomena (Vol. 143, Issues 1–4, pp. 1–20). Elsevier BV. https://doi.org/10.1016/s0167-2789(00)00094-4

Cabral, J., Hugues, E., Sporns, O., & Deco, G. (2011). Role of local network oscillations in resting-state functional connectivity. In NeuroImage (Vol. 57, Issue 1, pp. 130–139). Elsevier BV. https://doi.org/10.1016/j.neuroimage.2011.04.010

2. Reduced models

A reduced NMM is a mathematical simplification of a detailed and complex spiking neural network in which differential equations simulate the activity of individual cells often including different types, electrophysiological behaviours, and synaptic couplings. This set of N coupled equations (at least one per cell) is reduced through a mathematical technique called mean field reduction, to a small set of equations that captures the averaged behaviour of the whole population. Individual variability is usually neglected, however, the behaviour of different subpopulations of neurons (e.g., excitatory and inhibitory neurons) could be captured in the model with separated equations. This way, a reduced model could either result in a single differential equation or in a limited set of coupled differential equations including one per subpopulation. The parameters of the model, such as synaptic efficacies or time constants, are usually estimated or fitted based on experimental data.

The key idea behind the mean field reduction is to assume that the behaviour of each neuron is influenced primarily by the average activity of the other neurons, and therefore, just averaged firing rates or membrane potentials could describe the dynamics of the system.

2.1 Wong-Wang (2006)

The Wong-Wang model, proposed by Kong-Fatt Wong and Xiao-Jing Wang in 2006, is a mean-field reduction of a biophysically detailed spiking neural network developed to investigate the underlying parietal activity observed in binary decision-making experiments with monkeys (Wang, 2002; 01092-9)Wong & Wang, 2006). Their model integrated two pools of excitatory pyramidal cells, to encode two different stimuli associated with their decision-making context, and inhibitory interneurons (80%, 20%). These neurons modelled as integrate-and-fire including AMPA, NMDA and GABA types of synaptic coupling. The resulting reduced model included two differential equations to represent the averaged firing rate activity of each of the two pyramidal pools.

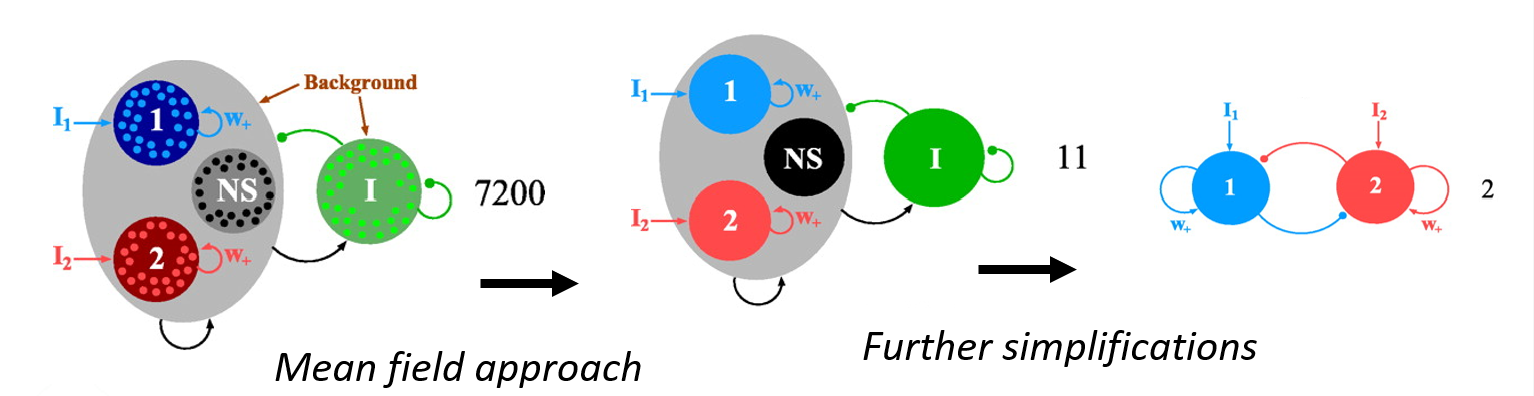
Later, the model was adapted to be implemented into a BNM, using just one differential equation (i.e., one pyramidal pool), to study resting-state fMRI activity (Deco, et al., 2013). This adaptation was the one implemented in TVB:

$$ \begin{gather} \dot S_i(t) = -\frac{S_i}{\tau_s} + (1 - S_i) \gamma H(x_i)+\sigma v_i(t)\\ H(x_i) = \frac{ax_i-b}{1- e^{-d(ax_i -b)}}\\ x_i = w J_N S_i + I_0 + G J_N \sum_{j=1}^{N} C_{ij} S_{j} \end{gather} $$

|Parameter|Value|Units|Description| |---------|-----|-----|-----------| |$\gamma$ |0.641| | Kinetic parameter| |$\tau_s$ |100 | ms | NMDA decay time constant| |$\sigma$ | $10^{-3}$| nA| Gaussian noise ($v_i$) amplitude| | | |a |0.27 | nC | Input gain parameter| |b |0.108| kHz | Firing rate baseline| |d | 154 |ms | Time constant for firing rate changes | | | |w | 0.9 | | Local excitatory recurrence| |$J_N$ |0.2609| nA | NMDA-mediated synaptic couplings| |$I_o$ | 0.3 | nA | Effective external input|

Where $S_i$ denotes average synaptic gating, $H(x_i)$ denotes population firing rate, and $v_i(t)$ denotes a Gaussian noise. The firing rate depends on $x_i$ (i.e., the input current), and is calculated through an input-output (i.e., current to firing rate) transfer function H with parameters a, b, and d.

## A2. Neural Mass Model
m = models.ReducedWongWang(
    gamma=np.array([0.641]), tau_s=np.array([100]),
    a=np.array([0.27]), b=np.array([0.108]), d=np.array([154]),
    w=np.array([0.9]), J_N=np.array([0.2609]), I_o=np.array([0.3]))


# A3. Coupling function - How NMMs will link through structural connectivity 
coup = coupling.Linear(a=np.array([0.1])) 


""" Integration time settings """
timescale, simLength, transient_t = "ms", 2000, 0  # timesteps in NMM's timescale; transient time to exclude
samplingFreq = 1  # Hz - datapoints / timestep 
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints

# A4. integrator: dt = timestep/datapoint = 1/samplingFreq(Hz=datapoints/timestep)
integrator = integrators.HeunStochastic(dt=1/samplingFreq, noise=noise.Additive(nsig = np.array([1e-3])))



## A1. Structural connectivity
conn = connectivity.Connectivity.from_file("paupau.zip")  # Loads structural connectivity
conn.weights = conn.scaled_weights(mode="tract")  # Scales number of streamlines using the max
conn.speed = np.array([3.9])  #(m/s) Defines conduction speed shaping delays



# B1. Configure simulation
tic0 = time.time()
sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

# B2. Run simulation
output = sim.run(simulation_length=simLength)
print("Simulation time: %0.2f sec  |  %0.2f sec/sim.%s" % 
      (time.time() - tic0, (time.time() - tic0)/simLength, timescale))


# C1. Extract data
raw_data = output[0][1][transient_dp:, 0, :, 0].T
raw_time = output[0][0][transient_dp:]

# C2. Plot signals and spectra
timeseries_spectra(raw_data, simLength, transient_t, conn.region_labels, yaxis=r"$S_i$",
                   timescale=timescale, mode="inline", title="Wong-Wang (2006)")

This model tends to a fixed point, so noise is needed to keep the system active. Deco's research showed how moderate levels of noise in combination with interregional coupling could lead to synchronous activations in the model.

Exercise 2. The noise have been proposed as bifurcation parameter for Wong-Wang model. Simulate, plot and explore the bifurcation diagram over noise.

""" Exercise 2. Bifurcation of Wong-Wang over noise - Re-use code."""

2.2 Stefanescu-Jirsa (2008)

In 2008, Roxana Stefanescu and Viktor Jirsa, published the reduction of two spiking neural networks built with phenomenological models of individual neurons behaviour: the Fitzhug-Nagumo (FHN) neuron model (FitzHugh, 1961; 86902-6) Nagumo et al., 1962) and Hindmarsh-Rose (HR) neuron model (Hindmarsh & Rose, 1984). FHN model reproduces the oscillatory behaviour of neurons through a set of two coupled differential equations, one representing the excitation of the system including the fast dynamics of action potentials and another representing the slow dynamics of recovery and repolarization processes. The HR model is an extension of the FHN model a similar structure (i.e., excitation and recovery variables) but incorporating an additional differential equation to account for neural adaptation mechanisms. This way the model captures a wider range of neural dynamics including regular spiking, but also bursting and chaotic behaviour. For the sake of brevity, we will focus here on the reduction of the HR model.

The spiking neural network built by Stefanescu & Jirsa (2008) consisted of 200 neurons (either FHN or HR), including 150 excitatory and 50 inhibitory and coupled linearly and instantaneously as gap junctions. Therefore, this network model does not account for phenomena related to slow chemical synaptic coupling. They used different coupling strengths for the connections within the excitatory population ($K_{11}$), from excitatory to inhibitory ($K_{21}$), and vice versa ($K_{12}$). Inhibitory-inhibitory connections were neglected as they are established with low probability.

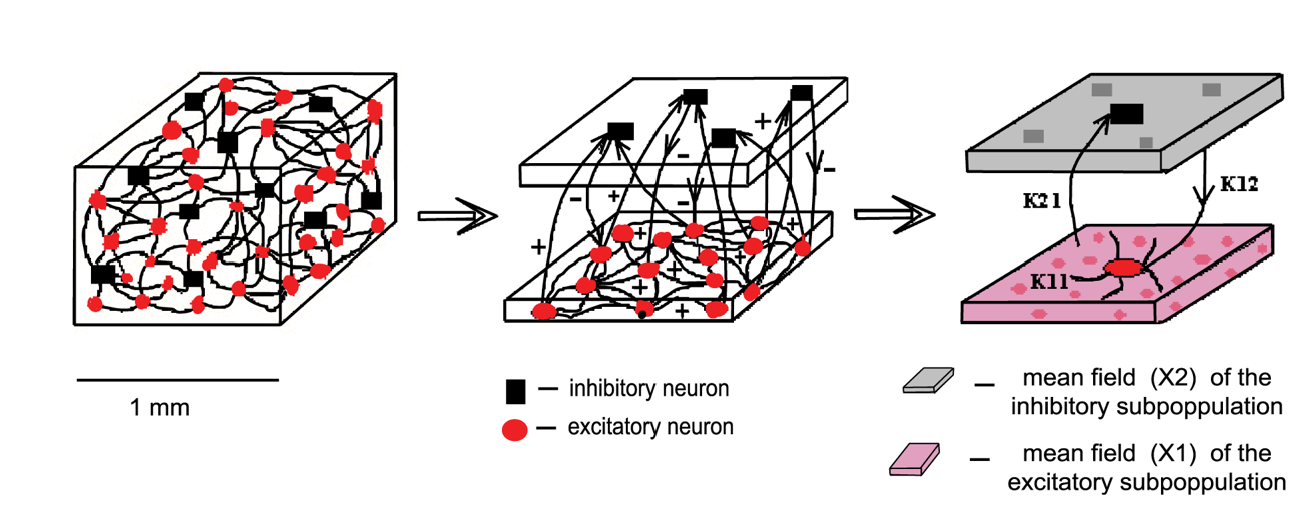
The only variable distinguishing between individual neurons was membrane excitability (I). This variable determines the neural behaviour for both FHN and HR models. For the HR model, it produces: I < 1.32 - fixed point dynamics; I > 1.32 - spike-burst behaviour; 2.92 < I < 3.40 - chaotic regime; and I > 3.4 simple oscillatory dynamics. All these types of behaviour were included in the reduced model by defining 3 modes of neural activity (i.e., small, medium, and high I values) that would be considered during the simulation of the model.

Following this rationale, they used the mean-field approach and a mode decomposition technique to derive two coupled sets (one excitatory, one inhibitory) of three differential equations (HR model):

$$ \dot{\xi_i} = \eta_i- a_i \xi_i^3 + b_i \xi_i^2 - \tau_i + K_{11} \left[\sum_{k=1}^{3} A_{ik} \xi_k - \xi_i \right] - K_{12} \left[ \sum_{k=1}^{3} B_{ik} \alpha_k - \xi_i \right] + I_{Ei} \\ \dot{\eta_i} = c_i - d_i \xi_i^2 - \eta_i \\ \dot{\tau_i} = r s \xi_i - r \tau_i - m_i $$

$$ \dot{\alpha_i} = \beta_i - e_i \alpha_i^3 + f_i \alpha_i^2-\gamma_i+K_{21} \left[\sum_{k=1}^{3} C_{ik} \xi_k - \alpha_i \right] + I_{Ii} \\ \dot{\beta_i} = h_i - p_i \alpha_i^2 - \beta_i \\ \dot{\gamma_i}=r s \alpha_i - r \gamma_i - n_i $$

Where $i, k \subset \{1,2,3\}$ represent the three modes of neural activity mentioned before (i.e., small, medium, and high I values). The use of $k$ modes serves to represent the interconnections between neurons operating in each of the three modes of activity, for instance, to represent the input from excitatory neurons in mode $k$=3 to excitatory neurons in mode $i$=1. Most parameters of the model are calculated from baseline values (see table below) following the results of the mode decomposition technique and using Gaussian distributions with $\mu$ and $\sigma$ parameters (see supplementary material in Stefanescu & Jirsa, 2008). Importantly, those calculations result in three increasing values of I, in line with the definition of the modes.

Parameter	Value	Description
a, b, c, d	1, 3, 1, 5	Fast ion channels parameters
r	0.006	Slow ion channels parameters
s	4	Bursting strength
K11	0.5	Local excitatory-excitatory synaptic coupling
K12	0.1	Local inhibitory to excitatory synaptic coupling
K21	0.15	Local excitatory to inhibitory synaptic coupling
$\mu$	3.3	Mean of input's (I) Gaussian distribution
$\sigma$	0.3	Standard deviation of input's (I) Gaussian distribution
$x_0$	-1.6	Leftmost equilibrium point of x

## A2. Neural Mass Model
m = models.ReducedSetHindmarshRose(
    mu=np.array([3.3]), sigma=np.array([0.3]),
    K11=np.array([0.5]), K12=np.array([0.1]), K21=np.array([0.15]),
    a=np.array([1]), b=np.array([3]), c=np.array([1]), d=np.array([5]),
    r=np.array([0.006]), s=np.array([4]), xo=np.array([-1.6]))


# A3. Coupling function - How NMMs will link through structural connectivity 
coup = coupling.Linear(a=np.array([0.1])) 


""" Integration time settings """
timescale, simLength, transient_t = "ms", 1000, 0  # timesteps in NMM's timescale; transient time to exclude
samplingFreq = 100  # Hz - datapoints / timestep 
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints

# A4. integrator: dt = timestep/datapoint = 1/samplingFreq(Hz=datapoints/timestep)
integrator = integrators.EulerStochastic(dt=1/samplingFreq, noise=noise.Additive(nsig = np.array([0])))



## A1. Structural connectivity
conn = connectivity.Connectivity.from_file("paupau.zip")  # Loads structural connectivity
conn.weights = conn.scaled_weights(mode="tract")  # Scales number of streamlines using the max
conn.speed = np.array([3.9])  #(m/s) Defines conduction speed shaping delays



# B1. Configure simulation
tic0 = time.time()
sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

# B2. Run simulation
output = sim.run(simulation_length=simLength)
print("Simulation time: %0.2f sec  |  %0.2f sec/sim.%s" % 
      (time.time() - tic0, (time.time() - tic0)/simLength, timescale))


# C1. Extract data
raw_data = output[0][1][transient_dp:, 0, :, 0].T
raw_time = output[0][0][transient_dp:]

# C2. Plot signals and spectra
timeseries_spectra(raw_data, simLength, transient_t, conn.region_labels, yaxis=r"$\xi_1$",
                   timescale=timescale, mode="inline", title="Stefanscu-Jirsa (2008)")

##  Phase plane
# C1. Extract data cutting initial transient
transient_t, cut_t = 0, 500  # simulated timesteps
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints
cut_dp = cut_t * samplingFreq

# Prepare the variables that feed in the phase plane
# output[monitor_id][time=0|data=1][timepoints, stateVars, ROIs, modes]
region_id = 0  # Select region of interest to plot its phase plane
subsample = 10  # Reduce memory load by subsampling the signal

x = output[0][1][transient_dp:cut_dp:subsample, 0, region_id, 0].T  
y = output[0][1][transient_dp:cut_dp:subsample, 1, region_id, 0].T 
z = output[0][1][transient_dp:cut_dp:subsample, 2, region_id, 0].T
t = output[0][0][transient_dp:cut_dp:subsample] 

                                                  # Unicodes for xi, eta and tau
timeseries_phaseplane(t, x, y, z, mode="inline", params=["\u03be", "\u03b7", "\u03c4"], speed=20)

References

Stefanescu, R. A., & Jirsa, V. K. (2008). A Low Dimensional Description of Globally Coupled Heterogeneous Neural Networks of Excitatory and Inhibitory Neurons. In K. J. Friston (Ed.), PLoS Computational Biology (Vol. 4, Issue 11, p. e1000219). Public Library of Science (PLoS). https://doi.org/10.1371/journal.pcbi.1000219

---

Falcon, M. I., Riley, J. D., Jirsa, V., McIntosh, A. R., Elinor Chen, E., & Solodkin, A. (2016). Functional Mechanisms of Recovery after Chronic Stroke: Modeling with the Virtual Brain. In eneuro (Vol. 3, Issue 2, p. ENEURO.0158-15.2016). Society for Neuroscience. https://doi.org/10.1523/eneuro.0158-15.2016

Triebkorn, P., Zimmermann, J., Stefanovski, L., Roy, D., Solodkin, A., Jirsa, V., Deco, G., Breakspear, M., McIntosh, A. R., & Ritter, P. (2020). Identifying optimal working points of individual Virtual Brains: A large-scale brain network modelling study. Cold Spring Harbor Laboratory. https://doi.org/10.1101/2020.03.26.009795

3. Biologically-informed models

A biologically-informed neural mass model aims to capture the dynamics of large-scale neural populations incorporating biophysical details and principles observed in real biology. This may include considerations of synaptic interactions, neural membrane dynamics, inhibitory-excitatory balance, and other factors that influence population-level dynamics. They represent populations of neurons as a single entity, characterized by variables such as average firing rates or membrane potentials. These models are often grounded in empirical observations and experimental data. They strive to reproduce or explain experimental findings, such as oscillations, evoked responses, or other population-level phenomena observed in neural recordings.

Despite trying to incorporate biophysical details, they involve simplifications and approximations. These models strike a balance between biological realism and computational feasibility, enabling researchers to gain a deeper understanding of large-scale brain dynamics and make predictions about neural activity under different conditions.

During the last thirty years of the 20th century, a set of extraordinary elegant scientific developments set the foundations of what we know today as biologically-informed neural masses. Indeed, even the reduced models presented earlier have some elements inherited from these older ones.

3.1 Wilson-Cowan (1972)

The model proposed in 1972 by Hugh R. Wilson and Jack D. Cowan was one of these relevant advances. They described the collective behaviour of populations of neurons based on their firing rate and highlighted the importance of the interaction between excitatory and inhibitory processes in the brain:

"all nervous processes of any complexity are dependent upon the interaction of excitatory and inhibitory cells". ... It was just this failure to consider inhibition that led Ashby et al. (1962) to conclude that the dynamical stability of the brain was paradoxical, and it was the introduction of inhibition by Griffith (1963) which dissolved the paradox. Consequently, we take it to be essential that there be both excitatory and inhibitory cells within any local neural population.

The model assumes that the behaviour of each population can be described by a single variable, representing the average firing rate of the neurons within that population. Therefore, the dynamics of each population are described by a set of differential equations that capture the balance between excitation and inhibition.

$$ \begin{gather} \tau_e \frac{dE}{dt} = -E + (k_e - r_eE) S_e(c_{ee} E - c_{ei} I + P)\\ \tau_i \frac{dI}{dt} = -I + (k_i - r_iI) S_i(c_{ie} E - c_{ii} I + Q) \end{gather} $$

Where:

$$ \begin{gather} S(x)=\frac{1}{1+e^{-a(x-\theta)}} - \frac{1}{1+e^{a\theta}} \end{gather} $$

Parameter	Value	Description
$k_e$, $k_i$	1, 1	Maximum of response function
$r_e$, $r_i$	0, 0	Refractory period
$\tau_e$, $\tau_i$	10, 20	Membrane time constants
$c_{ee}$	3.25	Excitatory to excitatory synaptic coupling
$c_{ei}$	2.5	Inhibitory to excitatory synaptic coupling
$c_{ie}$	3.75	Excitatory to inhibitory synaptic coupling
$c_{ii}$	0	Inhibitory to inhibitory synaptic coupling
P, Q	0.31, 0	External stimulus for excitatory and inhibitory, respectively
$a_e$, $a_i$	4, 4	Slope of the response function
$b_e$, $b_i$	1.8, 3	Position of maximum slope for the sigmoid function
$\theta_e$, $\theta_i$	0, 0	Excitatory/Inhibitory threshold

## A2. Neural Mass Model
m = models.WilsonCowan(P=np.array([0.31]), Q=np.array([0]),
                       a_e=np.array([4]), a_i=np.array([4]),
                       alpha_e=np.array([1]), alpha_i=np.array([1]),
                       b_e=np.array([1]), b_i=np.array([1]),
                       c_e=np.array([1]), c_ee=np.array([3.25]), c_ei=np.array([2.5]),
                       c_i=np.array([1]), c_ie=np.array([3.75]), c_ii=np.array([0]),
                       k_e=np.array([1]), k_i=np.array([1]),
                       r_e=np.array([0]), r_i=np.array([0]),
                       tau_e=np.array([10]), tau_i=np.array([20]),
                       theta_e=np.array([0]), theta_i=np.array([0]), 
                       variables_of_interest=["E", "I"])


# A3. Coupling function - How NMMs will link through structural connectivity (what variable to use and transformations to apply)
coup = coupling.Linear(a=np.array([0.25]))


""" Integration time settings """
timescale, simLength, transient_t = "ms", 2000, 1000  # timesteps in NMM's timescale; transient time to exclude
samplingFreq = 1  # Hz - datapoints / timestep 
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints



# B1. Configure simulation
tic0 = time.time()
sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

# B2. Run simulation
output = sim.run(simulation_length=simLength)
print("Simulation time: %0.2f sec  |  %0.2f sec/sim.%s" % 
      (time.time() - tic0, (time.time() - tic0)/simLength, timescale))


# C1. Extract data
raw_data = output[0][1][transient_dp:, 0, :, 0].T
raw_time = output[0][0][transient_dp:]

# C2. Plot signals and spectra
timeseries_spectra(raw_data, simLength, transient_t, conn.region_labels, yaxis="E (Hz)",
                   timescale=timescale, mode="inline", title="Wilson-Cowan (1972)")

""" Exercise 3. Build a phase plane for the Wilson-Cowan model. 
Use the parameters defined in the table above and the following code hints."""

References

Wilson, H. R., & Cowan, J. D. (1972). Excitatory and Inhibitory Interactions in Localized Populations of Model Neurons. In Biophysical Journal (Vol. 12, Issue 1, pp. 1–24). Elsevier BV. https://doi.org/10.1016/s0006-3495(72)86068-5

---

Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., & Kötter, R. (2009). Key role of coupling, delay, and noise in resting brain fluctuations. In Proceedings of the National Academy of Sciences (Vol. 106, Issue 25, pp. 10302–10307). Proceedings of the National Academy of Sciences. https://doi.org/10.1073/pnas.0901831106

Daffertshofer, A., & van Wijk, B. C. M. (2011). On the Influence of Amplitude on the Connectivity between Phases. In Frontiers in Neuroinformatics (Vol. 5). Frontiers Media SA. https://doi.org/10.3389/fninf.2011.00006

Abeysuriya, R. G., Hadida, J., Sotiropoulos, S. N., Jbabdi, S., Becker, R., Hunt, B. A. E., Brookes, M. J., & Woolrich, M. W. (2018). A biophysical model of dynamic balancing of excitation and inhibition in fast oscillatory large-scale networks. In D. Marinazzo (Ed.), PLOS Computational Biology (Vol. 14, Issue 2, p. e1006007). Public Library of Science (PLoS). https://doi.org/10.1371/journal.pcbi.1006007

Daffertshofer, A., Ton, R., Pietras, B., Kringelbach, M. L., & Deco, G. (2018). Scale-freeness or partial synchronization in neural mass phase oscillator networks: Pick one of two? In NeuroImage (Vol. 180, pp. 428–441). Elsevier BV. https://doi.org/10.1016/j.neuroimage.2018.03.070

3.2 Jansen-Rit (1995)

The Jansen-Rit model is a biologically-plausible NMM intended to reproduce the activity of a cortical column -including pyramidal cells (y0), excitatory (y1) and inhibitory (y2) interneurons- in terms of voltage by a set of second-order differential equations:

$$ \begin{gather} \dot y_{0_i}(t) = y_{3_i}(t) \label{eq:y0}\\ \dot y_{1_i}(t) = y_{4_i}(t) \label{eq:y1}\\ \dot y_{2_i}(t) = y_{5_i}(t) \label{eq:y2}\\ \dot y_{3_i}(t) = \frac{He}{taue} \cdot S[y_{1_i}(t) - y_{2_i}(t)] - \frac{2}{ taue} \cdot y_{3_i}(t) - \frac{1}{taue^2} \cdot y_{0_i}(t) \label{eq:y3}\\ \dot y_{4_i}(t) = \frac{He}{taue} \cdot (input(t) + C_{ep} \cdot S[C_{pe} \cdot y_{0_i}(t)]) - \frac{2}{taue} \cdot y_{4_i}(t) - \frac{1}{taue^2} \cdot y_{1_i}(t) \label{eq:y4}\\ \dot y_{5_i}(t) = \frac{Hi}{taui} \cdot (C_{ip} \cdot S[C_{pi} \cdot y_{0_i}(t)]) - \frac{2}{taui} \cdot y_{5_i}(t) - \frac{1}{taui^2} \cdot y_{2_i}(t) \label{eq:y5} \end{gather} $$

Where S[v] is a sigmoidal function that converts the population averaged voltage into firing rate:

$$ \begin{gather} S\left[v\right]\ =\ \frac{v_{\max}}{1\ +\ \exp^{r\left(v_0-v\right)}} \label{eq:sigmoid} \end{gather} $$

and the input(t) represents the sum of interregional afferences and intrinsic input ($p_i +\eta_i(t)$): $$ \begin{gather} input(t) = p_i + \eta_i(t) + g\sum_{j=1}^{n} w_{ji} \cdot S[y_{1_j}(t - d_{ji}) - y_{2_j}(t - d_{ji})] \end{gather} $$

Parameter	Value	Unit	Description
He	3.25	mV	Average excitatory synaptic gain
Hi	22	mV	Average inhibitory synaptic gain
taue	10	ms	Time Constant of excitatory PSP
taui	20	ms	Time Constant of inhibitory PSP
Cpe	135		Average synaptic contacts: pyramidals to excitatory interneurons
Cep	108		Average synaptic contacts: excitatory interneurons to pyramidals
Cpi	33.75		Average synaptic contacts: pyramidals to inhibitory interneurons
Cip	33.75		Average synaptic contacts: inhibitory interneurons to pyramidals
p	0.1085	$ms^{-1}$	Mean of random gaussian intrinsic input
$\eta$	0.022	$ms^{-1}$	Standard deviation of random gaussian intrinsic input (noise)
$v_{max}$	0.005	$ms^{-1}$	Maximum firing rate
r	0.56	$mV^{-1}$	Slope of the presynaptic function at $v_0$
$v_{0}$	6	mV	Potential when half the maximum firing rate is achieved
g	25		Coupling factor for inter-regional communication
s	3.9	mm/ms	Conduction speed for inter-regional communication

---

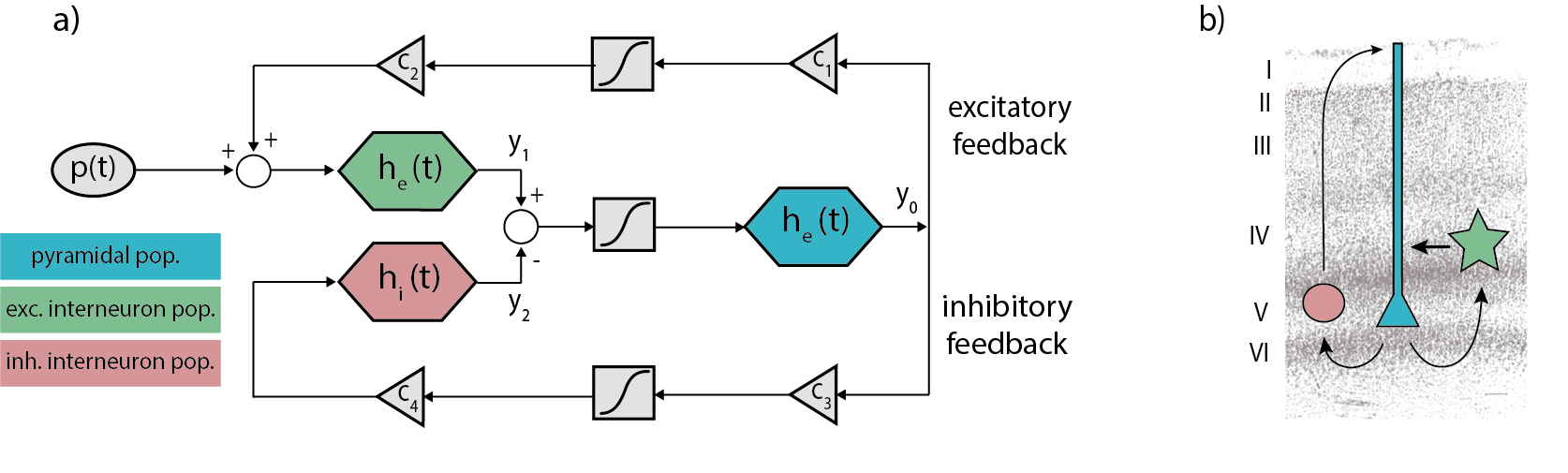
Figure 1 Schemes of the JR model. a) Block diagram depicting JR operators and modules where each color is associated with a different neural population: pyramidal (cyan), excitatory interneurons (green) and inhibitory interneuron (red). b) Histological contextualization of the cortical layers. Taken from Cabrera-Álvarez et al. (2023).

## A2. Neural Mass Model
m = JansenRit1995(He=np.array([3.25]), Hi=np.array([22]),
                  tau_e=np.array([10]), tau_i=np.array([20]),
                  c=np.array([1]), c_pyr2exc=np.array([135]), c_exc2pyr=np.array([108]),
                  c_pyr2inh=np.array([33.75]), c_inh2pyr=np.array([33.75]),
                  p=np.array([0.1085]), sigma=np.array([0.22]),
                  e0=np.array([0.005]), r=np.array([0.56]), v0=np.array([6]))

# A3. Coupling function - How NMMs will link through structural connectivity (what variable to use and transformations to apply)
coup = coupling.SigmoidalJansenRit(a=np.array([10]), cmax=np.array([0.005]),  midpoint=np.array([6]), r=np.array([0.56]))


""" Integration time settings """
timescale, simLength, transient_t = "ms", 2000, 500  # timesteps in NMM's timescale; transient time to exclude
samplingFreq = 1  # Hz - datapoints / timestep 
transient_dp = transient_t * samplingFreq  # convert transient time into number of datapoints

# A4. integrator: dt = timestep/datapoint = 1/samplingFreq(Hz=datapoints/timestep)
integrator = integrators.EulerStochastic(dt=1/samplingFreq, noise=noise.Additive(nsig = np.array([0])))


# B1. Configure simulation
tic0 = time.time()
sim = simulator.Simulator(model=m, connectivity=conn, coupling=coup,  integrator=integrator, monitors=mon)
sim.configure()

# B2. Run simulation
output = sim.run(simulation_length=simLength)
print("Simulation time: %0.2f sec  |  %0.2f sec/sim.%s" % 
      (time.time() - tic0, (time.time() - tic0)/simLength, timescale))


# C1. Extract data
raw_data = output[0][1][transient_dp:, 0, :, 0].T
raw_time = output[0][0][transient_dp:]

# C2. Plot signals and spectra
timeseries_spectra(raw_data, simLength, transient_t, conn.region_labels, yaxis="Voltage (mV) <br> y0",
                   timescale=timescale, mode="inline", title="Jansen-Rit (1995)")

See its phase plane and bifurcation diagram in the Brain Network Model tutorial.

References

Jansen, B. H., & Rit, V. G. (1995). Electroencephalogram and visual evoked potential generation in a mathematical model of coupled cortical columns. In Biological Cybernetics (Vol. 73, Issue 4, pp. 357–366). Springer Science and Business Media LLC. https://doi.org/10.1007/bf00199471

---

Stefanovski, L., Triebkorn, P., Spiegler, A., Diaz-Cortes, M.-A., Solodkin, A., Jirsa, V., McIntosh, A. R., & Ritter, P. (2019). Linking Molecular Pathways and Large-Scale Computational Modeling to Assess Candidate Disease Mechanisms and Pharmacodynamics in Alzheimer’s Disease. In Frontiers in Computational Neuroscience (Vol. 13). Frontiers Media SA. https://doi.org/10.3389/fncom.2019.00054

Kazemi, S., & Jamali, Y. (2022). Phase synchronization and measure of criticality in a network of neural mass models. In Scientific Reports (Vol. 12, Issue 1). Springer Science and Business Media LLC. https://doi.org/10.1038/s41598-022-05285-w

Kuhlmann, L., Freestone, D. R., Manton, J. H., Heyse, B., Vereecke, H. E. M., Lipping, T., Struys, M. M. R. F., & Liley, D. T. J. (2016). Neural mass model-based tracking of anesthetic brain states. In NeuroImage (Vol. 133, pp. 438–456). Elsevier BV. https://doi.org/10.1016/j.neuroimage.2016.03.039

Sohanian Haghighi, H., & Markazi, A. H. D. (2019). Dynamic origin of spike and wave discharges in the brain. In NeuroImage (Vol. 197, pp. 69–79). Elsevier BV. https://doi.org/10.1016/j.neuroimage.2019.04.047

Forrester, M., Crofts, J. J., Sotiropoulos, S. N., Coombes, S., & O’Dea, R. D. (2020). The role of node dynamics in shaping emergent functional connectivity patterns in the brain. In Network Neuroscience (Vol. 4, Issue 2, pp. 467–483). MIT Press - Journals. https://doi.org/10.1162/netn_a_00130