Jansen-Rit's bifurcation

Neural population models like the Jansen-Rit (JR) reveal complex phase transitions (bifurcation) when tuning key parameters. The classical bifurcation parameter of the JR is average external input to the cortical column (p), but there are others that contribute as well. In a previous post, we explored the bifurcation over global coupling (scales SC matrix). In this post, I combine the exploration of this parameter p with another less studied: C, the average number of synapses connecting subpopulations.

The role of average input (p) and synaptic coupling (C) in cortical dynamics

The impact of p in the model’s behaviour appears intuitive to me: if there is not enough input to the cortical column, the neurons do not activate; once the input reaches a certain threshold, neurons start to activate and the circuit switches on. From the architecture of the JR with default parameters, it could be derived that the circuit is capable of generating alpha activity -within a limit cycle- due to the interaction between excitatory and inhibitory populations. This interaction results into autonomous oscillations that in the classical parameterization appears first as a slow signal (~4 Hz), and with higher input as a faster one in alpha band (~10 Hz). Finally, when the input to the cortical column is too high, the oscillations dissapear and the activity becomes desynchronized -the limit cycle closes-. These are the behaviours we can see in the bifurcation through p. The model is an abstraction but: does it reproduce physiologically plausible behaviour?

In contrast, parameter C controls the overall strength of synaptic interactions within a cortical column. We could interpret this as making the circuit more intensly connected in all directions: excitatory to inhibitory, and viceversa. What we see in the figure is that as C decreases from its classical parameterization value (135), the model reduces the amplitude and presence of the limit cycles.

Jansen-Rit equations

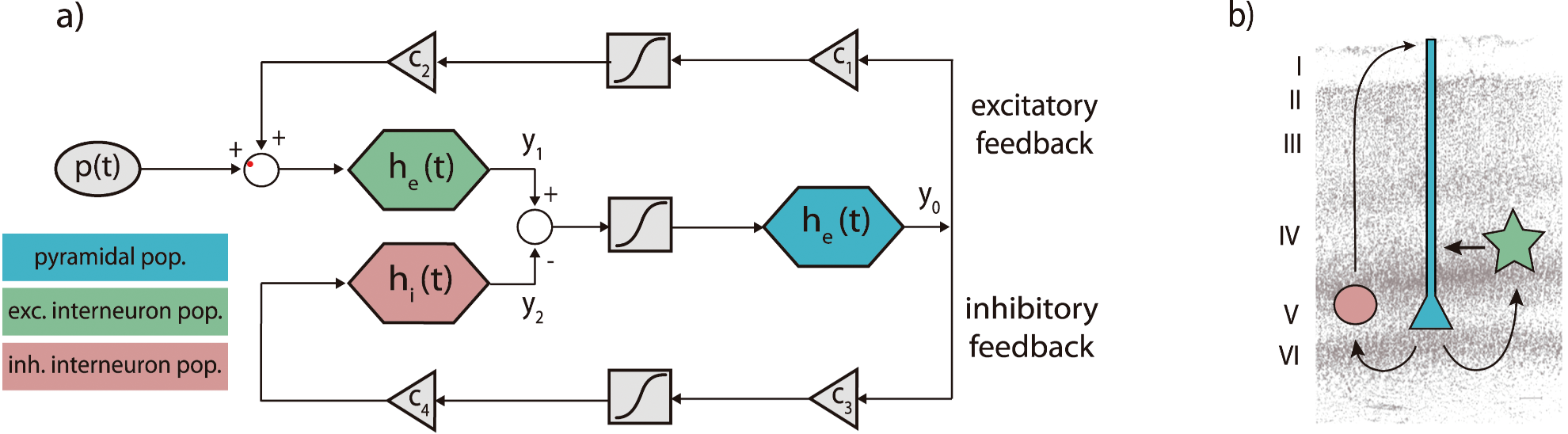
The Jansen-Rit model describes the dynamics of a cortical column with three interacting neuronal populations: pyramidal cells, excitatory interneurons, and inhibitory interneurons. The model equations are:

\[\begin{aligned} \dot{y}_0(t) &= y_3(t) \\ \dot{y}_3(t) &= A a S(y_1(t) - y_2(t)) - 2a y_3(t) - a^2 y_0(t) \\ \dot{y}_1(t) &= y_4(t) \\ \dot{y}_4(t) &= A a \left[ p(t) + C_2 S(C_1 y_0(t)) \right] - 2a y_4(t) - a^2 y_1(t) \\ \dot{y}_2(t) &= y_5(t) \\ \dot{y}_5(t) &= B b C_4 S(C_3 y_0(t)) - 2b y_5(t) - b^2 y_2(t) \end{aligned}\]

Where:

• $ y_0(t) $ is the membrane potential of the pyramidal population
• $ y_1(t) $, $ y_2(t) $ are the excitatory and inhibitory inputs to the pyramidal cells
• $ y_3(t) $, $ y_4(t) $, $ y_5(t) $ are the corresponding derivatives
• $ A, B $: average excitatory and inhibitory synaptic PSP gains
• $ a, b $: inverse time constants
• $ C_1, C_2, C_3, C_4 $: synaptic connectivity constants scaled by C
• $ p(t) $: external input (e.g., thalamic)
• $ S(v) $: sigmoid function converting membrane potential to firing rate: \(S(v) = \frac{2 e_0}{1 + \exp\left[ r (v_0 - v) \right]}\)

Takeaways

This analysis highlights how intrinsic synaptic coupling (C) governs cortical excitability and transitions between quiescence and rhythmic activity. Future work could explore how parameter C interacts with external inputs or structural connectivity to refine predictions about cortical state transitions in health and disease.

Let me know what you think—play with the interactive figure and share your insights!