JR equations for psychologists

Nowadays, computational neuroscience brings together experts from a wide range of backgrounds: physicists, mathematicians, engineers, biologists and, lately, also psychologists like myself. There will always be room for questions such as “how did a psychologist end up doing this?”. My answer would be that I was looking for accuracy in how we understand cognition. The search led me to the brain, then to the crucial role of mathematics. Then, it came coding, and I love it.

In this post, I’d like to share my psychologist-friendly approach to expressing the Jansen-Rit equations. This formulation was inspired by the one used by Spiegler et al. (2010), and I used it in a recent eNeuro publication (Cabrera-Álvarez, 2024). It goes like this:

\[\begin{aligned} \dot y_{0_i} &= y_{3_i} \\ \dot y_{1_i} &= y_{4_i} \\ \dot y_{2_i} &= y_{5_i} \\ \dot y_{3_i} &= \frac{H_e}{\tau_e} \, S\left(y_{1_i} - y_{2_i}\right) - \frac{2}{\tau_e} \, y_{3_i} - \frac{1}{\tau_e^2} \, y_{0_i} \\ \dot y_{4_i} &= \frac{H_e}{\tau_e} \left[ I_i(t) + C_{ep} \, S(C_{pe} \, y_{0_i}) \right] - \frac{2}{\tau_e} \, y_{4_i} - \frac{1}{\tau_e^2} \, y_{1_i} \\ \dot y_{5_i} &= \frac{H_i}{\tau_i} \, C_{ip} \, S(C_{pi} \, y_{0_i}) - \frac{2}{\tau_i} \, y_{5_i} - \frac{1}{\tau_i^2} \, y_{2_i} \end{aligned}\]

Post-synaptic potentials are now represented by $H$, referring to the impulse response function $h(t)$ that transforms firing rate into membrane voltage. Time constants are denoted by $\tau$, a conventional symbol used when describing synaptic dynamics. Additionally, the parameters governing synaptic connectivity are subscripted using a “from-to” convention—e.g., $C_{pe}$ indicates projections from pyramidal cells to excitatory interneurons. Take a look at the schematic below:

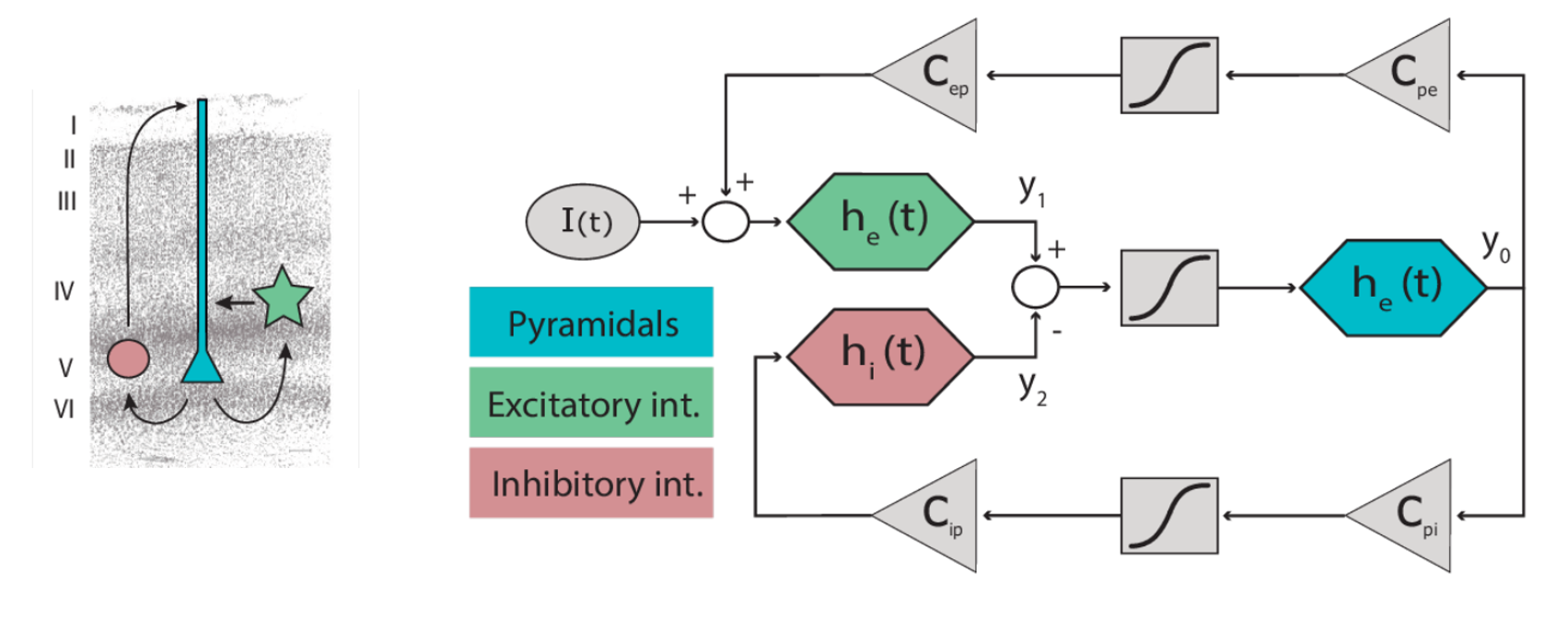
The sigmoidal activation function, the function that converts voltage into firing rate, did not change: \(S[v] = \frac{2 e_0}{1 + e^{r (v_0 - v)}}\)

And for the input to the system, we used $\eta$ for noise, representing $\mathcal{N}(p, \sigma)$ a white noise derived from a gaussian distribution with $p$ mean and $\sigma$ std. \(I_i(t) = \eta_i(t) + g \sum_{j=1}^{N} w_{ji} \, S\left[y_{1_j}(t - d_{ji}) - y_{2_j}(t - d_{ji})\right]\)

Conduction delays between regions is given by $d_{ji} = \frac{L_{ji}}{s}$.

Take a look to the parameters and their descriptions:

Parameter	Value	Unit	Description
$H_e$	3.25	mV	Average excitatory synaptic gain
$H_i$	22	mV	Average inhibitory synaptic gain
$\tau_e$	10	ms	Time constant of excitatory PSP
$\tau_i$	20	ms	Time constant of inhibitory PSP
$C_{pe}$	135	–	Synaptic contacts: pyramidals → excitatory interneurons
$C_{ep}$	108	–	Synaptic contacts: excitatory interneurons → pyramidals
$C_{pi}$	33.75	–	Synaptic contacts: pyramidals → inhibitory interneurons
$C_{ip}$	33.75	–	Synaptic contacts: inhibitory interneurons → pyramidals
$e_0$	0.0025	ms$^{-1}$	Half of the maximum firing rate
$r$	0.56	mV$^{-1}$	Slope of the sigmoid at $v_0$
$v_0$	6	mV	Membrane potential for half-maximum firing rate
$p$	0.1085	ms$^{-1}$	Mean of intrinsic noisy input
$\sigma$	0.022	ms$^{-1}$	Standard deviation of intrinsic noise