A NMM for epilepsy

Epilepsy is a neurological disorder characterized by recurrent seizures that arise from abnormal, excessive, and often synchronized neural activity. Beyond its clinical implications, epilepsy provides a compelling example of a complex dynamical system capable of spontaneously transitioning between distinct functional states—most notably from normal ( interictal) to pathological (ictal) activity. These transitions are not random but can be systematically studied using tools from nonlinear dynamics, bifurcation theory, and network science.

In this post, I introduce a recently developed neural mass model of epilepsy that builds upon the Jansen-Rit (JR) framework, specifically extending the Wendling-class formulation (Wendling et al., 2002). Wendling’s key contribution to the JR was the incorporation of a second inhibitory subpopulation into the original Jansen-Rit framework, distinguishing between fast, soma-targeting interneurons (typically associated with parvalbumin-positive cells) and slow, dendrite-targeting interneurons (such as somatostatin-positive cells). This modification enabled the model to reproduce more realistic dynamics of epileptic discharges, particularly the low-voltage fast activity characteristic of seizure onset.

Building on this foundation, López-Sola et al. (2022) introduced a physiologically grounded mechanism for chloride accumulation in pyramidal neurons, allowing the model to simulate the pathological shift of GABAergic inhibition into depolarizing (excitatory) influence. This addition makes the model autonomous and capable of generating seizure-like transitions driven solely by stochastic fluctuations and internal ionic dynamics. Cool!

Also, they approach the electrophysiological equations from a modular perspective that make it simpler to understand and modify (Sanchez-Todo, 2023). This implies using one second-order differential equation for each synapse, instead of one per subpopulation as in the JR. Cooler!

Model Architecture

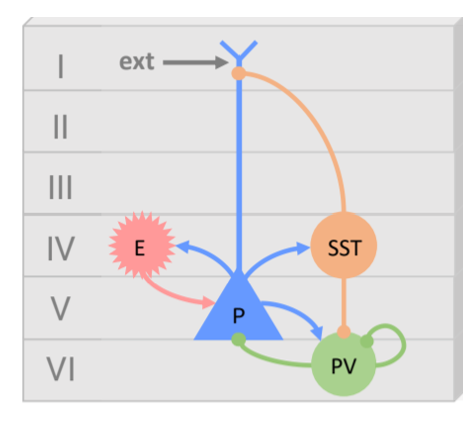
The model includes four interacting neuronal populations:

• Pyramidal cells (P): Main excitatory output

• Excitatory interneurons (E): Represent lateral excitation (e.g., spiny stellate)

• PV interneurons (PV): Fast GABAergic inhibition (soma-targeting)

• SST interneurons (SST): Slow GABAergic inhibition (apical dendrite-targeting)

Electrophysiological dynamics

Each synapse converts the presynaptic subpopulation’s firing rate $S(t)$ into a postsynaptic potential $v$ using the following second-order differential equation:

\[\begin{align} \dot v_{f\to t} &= x_{f\to t} \\ \dot x_{f\to t} &= \frac{H_f}{\tau_f} C_{f\to t} S_f(t)- \frac{2}{\tau_f} \, x_{f\to t} - \frac{1}{\tau_f^2} \, v_{f\to t} \\ \end{align}\]

Where the subscripts ft correspond to the convention from-to (from presynaptic subpopulation f, to postsynaptic subpopulation t). We will use:

• p for pyramidal cells
• e for excitatory interneurons
• sst for slow inhibition mediated by SST cells
• pv for fast inhibition mediated by PV cells.

Following the previous connectivity scheme, the model considers 8 intra-columnar connections:

\[\begin{align} \dot v_{p\to e} &= x_{p\to e} \\ \dot x_{p\to e} &= \frac{H_e}{\tau_e} C_{p\to e} S_p(t)- \frac{2}{\tau_e} \, x_{p\to e} - \frac{1}{\tau_e^2} \, v_{p\to e} \\ \\ \dot v_{p\to sst} &= x_{p\to sst} \\ \dot x_{p\to sst} &= \frac{H_e}{\tau_e} C_{p\to sst} S_p(t)- \frac{2}{\tau_e} \, x_{p\to sst} - \frac{1}{\tau_e^2} \, v_ {p\to sst} \\\\ \dot v_{p\to pv} &= x_{p\to pv} \\ \dot x_{p\to pv} &= \frac{H_e}{\tau_e} C_{p\to pv} S_p(t)- \frac{2}{\tau_e} \, x_{p\to pv} - \frac{1}{\tau_e^2} \, v_ {p\to pv} \\\\ \dot v_{e\to p} &= x_{e\to p} \\ \dot x_{e\to p} &= \frac{H_e}{\tau_e} C_{e\to p} S_e(t)- \frac{2}{\tau_e} \, x_{e\to p} - \frac{1}{\tau_e^2} \, v_{e\to p} \\\\ \dot v_{sst\to p} &= x_{sst\to p}\\ \dot x_{sst\to p} &= \frac{H_{sst}}{\tau_{sst}} C_{sst\to p} S_{sst}(t)- \frac{2}{\tau_{sst}} \, x_{sst\to p} - \frac{1}{\tau_{sst}^2} \, v_{sst\to p} \\\\ \dot v_{pv\to p} &= x_{pv\to p}\\ \dot x_{pv\to p} &= \frac{H_{pv}}{\tau_{pv}} C_{pv\to p} S_{pv}(t)- \frac{2}{\tau_{pv}} \, x_{pv\to p} - \frac{1}{\tau_ {pv}^2} \, v_{pv\to p} \\\\ \dot v_{sst\to pv} &= x_{sst\to pv}\\ \dot x_{sst\to pv} &= \frac{H_{sst}}{\tau_{sst}} C_{sst\to pv} S_{sst}(t)- \frac{2}{\tau_{sst}} \, x_{sst\to pv} - \frac{1}{\tau_{sst}^2} \, v_{sst\to pv} \\\\ \dot v_{pv\to pv} &= x_{pv\to pv}\\ \dot x_{pv\to pv} &= \frac{H_{pv}}{\tau_{pv}} C_{pv\to pv} S_{pv}(t)- \frac{2}{\tau_{pv}} \, x_{pv\to pv} - \frac{1}{\tau_{pv}^2} \, v_{pv\to pv} \\ \end{align}\]

and one for external inputs:

\[\begin{align} \dot v_{ext\to p} &= x_{ext\to p}\\ \dot x_{ext\to p} &= \frac{H_{e}}{\tau_{e}} C_{ext\to p} I(t)- \frac{2}{\tau_{e}} \, x_{ext\to p} - \frac{1}{\tau_{e}^2} \, v_{ext\to p} \\ \end{align}\]

with

\[\begin{align} I_i(t) = \eta_i(t) + g \sum_{j=1}^{N} w_{ji} \, S\left[v_{p_j}(t - d_{ji}))\right] \end{align}\]

we used $\eta$ for noise, representing $\mathcal{N}(p, \sigma)$ a white noise derived from a gaussian distribution with $p$ mean and $\sigma$ std. Conduction delays between regions is given by $d_{ji} = \frac{L_{ji}}{s}$. The sigmoid function converting voltage into firing rate follows:

\[\begin{align} S[v] = \frac{2 e_0}{1 + e^{r (v_0 - v)}} \end{align}\]

Where $v$ stands for the post-synaptic membrane potential calculated as the sum of incoming synaptic potentials for each t subpopulation:

\[\begin{align} v_p &= v_{e\to p} + v_{sst\to p} + v_{pv\to p} + v_{ext\to p}\\ v_e &= v_{p\to e}\\ v_{sst} &= v_{p\to sst}\\ v_{pv} &= v_{p\to pv} + v_{sst\to pv} + v_{pv\to pv}\\ \end{align}\]

Chloride Accumulation Dynamics

To model depolarizing GABAergic effects, the authors introduce chloride dynamics in pyramidal cells. Higher concentrations of chloride ($[Cl^-]$) in pyramidal cells reduces the effectiveness of GABAergic inhibition. The concentration is calculated separately for the soma (PV synapses) and dendrites (SST synapses) as the concentration depends strongly on the volume of the compartment being filled with chloride. The idea is that $[Cl^-]$ increases due to the synaptic activity of inhibitory cells on pyramidal neurons - that introduce chloride in the cell to hyperpolarize them-, and decreases due to the activity of chloride extrusion pumps such as the potassium-chloride cotransporter ( KCC2). In epilepsy these pumps might become altered and the balance between the intrusion and extrusion breaks.

Then, for each location (i.e., loc = [soma, dendrites]) the intracellular concentration of chloride follows:

\[\begin{align} \dot {[Cl^-]}_{loc} = \alpha^{\text{loc}}_{\mathrm{vol}} (I^{\text{loc}}_{\text{KCC2}} + I^{\text{loc}}_{\phi}) \end{align}\]

With:

\[\begin{align} I^{\text{loc}}_{\text{KCC2}} = -\alpha^{\text{loc}}_{\text{KCC2}} \left( E^{\text{loc}}_{\mathrm{Cl}^-}(t) - E_{K^+} \right) \end{align}\] \[\begin{align} I^{\text{loc}}_{\phi} = \alpha^{\text{loc}}_\phi \ \psi_{f}(t) \left( E^{\text{loc}}_{\mathrm{Cl}^-}(t) - V_m \right) \end{align}\]

With chloride reversal potential from the Nernst equation:

\[\begin{align} E_{\mathrm{Cl}^-}(t) = \frac{RT}{F} \ln \left( \frac{[\mathrm{Cl}^-]_i(t)}{[\mathrm{Cl}^-]_o} \right) \end{align}\]

And a filtered version of the firing rate of inhibitory subpopulations $\psi$:

\[\begin{align} \dot \psi_{f}(t) = \frac{C_{f\to p}}{\tau_{f}} S_{f}(t) - \frac{1}{\tau_f} \psi_f(t) \end{align}\]

With f subscripts again denoting the afferent inhibitory subpopulation that is targeting pyramidal cells including SST and PV cells. Finally, the amplitude of the IPSP becomes dynamic and is updated following:

\[\begin{align} H_{sst}(t) = w_0^{d} (E^{d}_{\text{GABA}}(t) - V_m) + H_{sst} \\ \\ H_{pv}(t) = w_0^{s} (E^{s}_{\text{GABA}}(t) - V_m) + H_{pv} \end{align}\]

Where:

\[\begin{align} E_{\text{GABA}}^{\text{loc}}(t) = \frac{RT}{F} \ln \left( \frac{4[Cl^-]_i^{\text{loc}}(t) + [HCO_3^-]_i }{ 4[Cl^-]_o + [HCO_3^-]_o} \right) \end{align}\]

Parameter	Value	Unit	Description
$H_e$	3.25	mV	Amplitude of the PSP for excitatory cells
$H_{sst}$	-22	mV	Amplitude of the PSP for SST cells
$H_{pv}$	-10	mV	Amplitude of the PSP for PV cells
$\tau_e$	5.5	ms	PSP time constant for excitatory cells
$\tau_{sst}$	20	ms	PSP time constant for SST cells
$\tau_{pv}$	2	ms	PSP time constant for PV cells
$c_{e \to p}$	108	—	Synaptic contacts: from excitatory interneurons to P
$c_{sst \to p}$	33.75	—	Synaptic contacts: from SST to P
$c_{pv \to p}$	108	—	Synaptic contacts: from PV to P
$c_{ext \to p}$	135	—	Synaptic contacts: from external input to P
$c_{p \to e}$	135	—	Synaptic contacts: from P to excitatory interneurons
$c_{p \to sst}$	33.75	—	Synaptic contacts: from P to SST
$c_{p \to pv}$	40.5	—	Synaptic contacts: from P to PV
$c_{sst \to pv}$	13.5	—	Synaptic contacts: from SST to PV
$c_{pv \to pv}$	270	—	Synaptic contacts: from PV to PV
$e_0$	0.005	ms$^{-1}$	Maximum firing rate
$r$	0.56	mV$^{-1}$	Slope of the sigmoid at $v_0$
$v_0$	6	mV	Membrane potential for half-maximum firing rate
$p$	0.4	ms$^{-1}$	Mean of intrinsic noisy input
$\sigma$	0.001	ms$^{-1}$	Standard deviation of intrinsic noise
$\alpha^d_{vol}$	0.0001	$\frac{\mathrm{mM}/\mathrm{ms}}{\mu\mathrm{A}/\mathrm{cm}^2}$	Chloride accumulation rate in dendrite
$\alpha^d_{kcc2}$	1	mS/cm$^2$	KCC2 efficiency dendrite
$\alpha^d_{\phi}$	1000	s·mS/cm$^2$	GABAergic flux rate dendrite
$w_0^d$	variable	—	Weight of pathological SST current
$\alpha^s_{vol}$	0.00001	$\frac{\mathrm{mM}/\mathrm{ms}}{\mu\mathrm{A}/\mathrm{cm}^2}$	Chloride accumulation rate in soma
$\alpha^s_{kcc2}$	10	mS/cm$^2$	KCC2 efficiency soma
$\alpha^s_{\phi}$	1000	s·mS/cm$^2$	GABAergic flux rate soma
$w_0^s$	variable	—	Weight of pathological PV current
$R$	8.314	J/(mol·K)	Universal gas constant
$T$	298	K	Absolute temperature
$F$	96.485	C/mmol	Faraday constant
$V_m$	-65	mV	Membrane potential
$E_K$	-85	mV	K reversal potential
$[Cl^-]_o$	150	mM	Extracellular Cl⁻ concentration
$[HCO_3^-]_o$	25	mM	Extracellular HCO₃⁻ concentration
$[HCO_3^-]_i$	15	mM	Intracellular HCO₃⁻ concentration